Для бруса построить эпюры 3 вариант
Построение эпюр продольных сил — формулы, условия и примеры решения задач
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
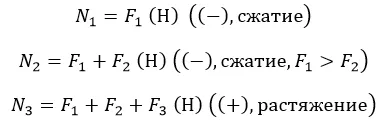
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
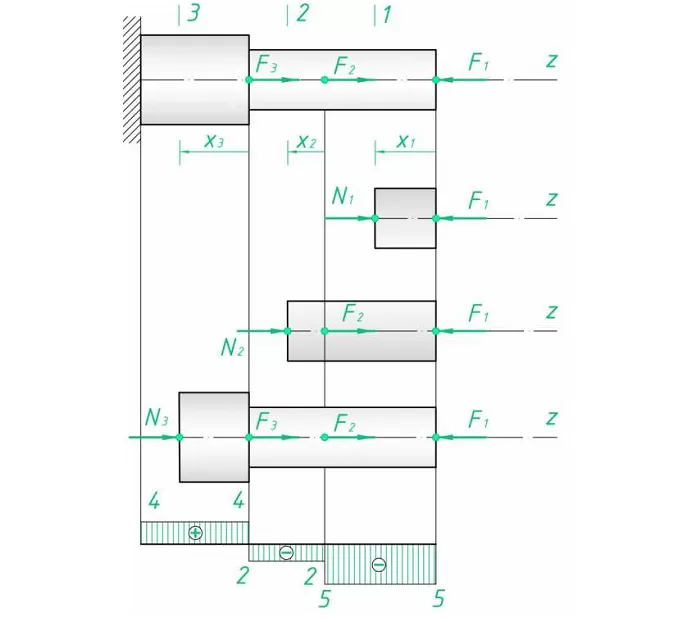
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
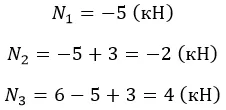
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
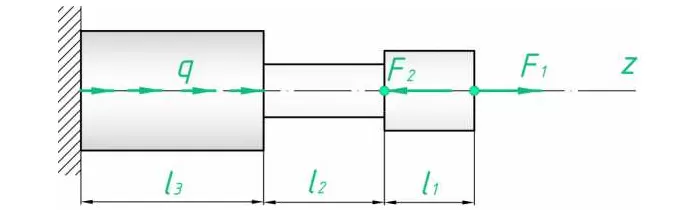
Рис. 2
Дано:
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
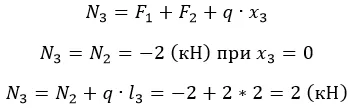
По полученным данным строим эпюру (рис. 3).
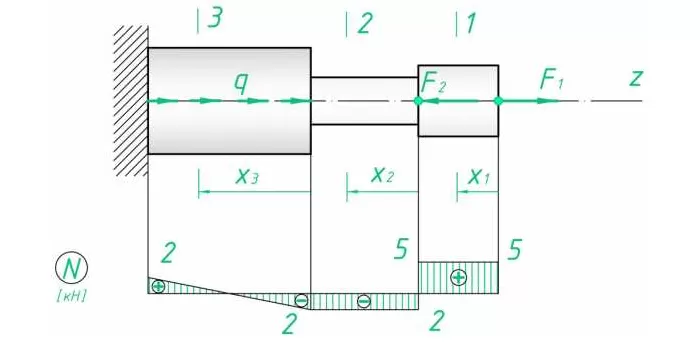
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
XP
¶»Û@ê4 5é+ͤqd ðÇÊhHY¡ÑÖ1%T É3%môÒ¡¤S&Æ×)ð@bÊSÄ·$ôCc
ÒP¡§Ú1m$ÅÐ%¥©a3ÒGI2£©Ò(fÀÆ{+Q2TB`AL_»4ï9bFÆ3P*Þ(Å
@)P>hMHA¡óaÅaL´ÀÆE±~ÀDÀ6bÁ@`,,Æ°,,Æp,°Là,Yàx-0Ç2}óMú&(öNü®¨feYÕËôúé±H/NÒÖù}:GU×eu¶úµÜ]íýþGrÜ&UR&ï&ÇÉ,9Ç«I#, OdÂ^_¿¸ÀëÔ®»éÕÇw5Å9¨êOeõa?½Ä`¯ÅC±ª1J;~:ÛY¤½m&éFpà[!l¬ÌF ZA·i
Ö³j=«Ö³j=«Ö³n=ëÖ³n=ëÖ³n=ëÖ³çÙA3¥ð*=¼¢Lñ%?,+d!½a«ÑdKÌÓ3éiz¾-nëÌÇéì4pï=Îq6:0×ÉÜÖñûÅêCæ`µ*ëýý L@ǼÜí¹t#QãHì$X`nÓ¬o(ÅEøGâ±Þqè°#;fÌuÃë¬;0$L¯ 7;v¬C²zìØQ$ ¦#ÑX³C;ù97DNG¢4WvÕcÇ#QÓÇe
dõØ ãHôd$$vzìh2eú&Îð°£²Õ£Gï²0}ÅÇ>÷;~À!]=~äø6v:£¸ÛVrÙ’h|
éû,¾fqÛ!È _}Æ7ZðÓ¡HÁ¡CB¾úï´&dá¦CTÜ÷ ßjÅy®w|õ ßk¼Uí2ùê4¾ÙZ5½*Ær¹#ÈXáOÐønkõt(ZpÑ!È _ý··ñÝÖéPp
Aùê¤Æw[;}·ÕÁqß!HZ®z©¿ßm/.Ù¯ùr½Ôå9½l.¯Î5꯫O®ê¼.Òò±oÒXßÆ’éÑÙñUAOÑlGùãi±¸OÏ@!Òã¢Q}
=t:[æ÷k|«úð°ü-{Øh¾¢Z jýpó8:Ë˧½ëÅC±foOìmù¯^6ceAM¤l?Ý¢61=ÿîôìüõWÑM¢ÅåÕùuÔÀÊõíûôMY=äËxë¦iåY/·«ûeÁp.ÕÅÃÌoJ@ªEµxľ2ý©]¬Åa¾.Hç¯ãSÖètÓ¢^»ÕýÞÙfQ?½DnïëºzÚ;¸+ßÔ>>6ÍfèáºÏÓÖ(=¾iJü`ó5
ÓƤBÉtRJo2p»Ã&dxf-6ñÎã¸bVJ¼ç2Åq/hÏ*ó>lîQ»$ãÙfnò¶ØNø96bn
ÊLüDp³U8UE#ã=$Îdlö5ÌÑ.Ã3n{´|ÖtuÅöL6F»([ýÛ1ÍÃXÊeÍc»ø©lé{!, ³ f>ÿBÞ¹{ãC½u¿ÎP¾^ÝwÈàW§ÛrS
Ez]þ°Z RA+£¨ÛÒ÷ÐèÑæ¿Z3²·f¾ý¯kf8þ¶Â7ÕÁj½Ø^ÏÕº>zWL«þÔ7M~ßçlÇvÄTë¡ÍXÜÕï×M[søøDzÁ4J:^ F$Ó_±©÷ÿ¤Kÿ;ÿ´`âBÁÿ(#%ßzÅ6¢hJ4ÖÚì°®~ëEü«Uvqt²¦y§wKàâèü8g
[?ýü¥å%[}.ñ)×å
®¿ôë¨Ð¶0 :*`U6YlÀÀ`$ùÌC:êyÞfPGÿCe£ÜøéêÐöý,ôÓ|NlsnTGAÎM7}QÒébÆ>kHôøüz¦#à fpÏêçëO Áаé
endstream
endobj
1100 0 obj
>stream
hÞTOO0Åï|9jÿDVï¥DJSØß^ÚAJÞ¯Ìá
«Î§³íg`o~Ô5ÎÐöÖxÆ«×
v½.ÀôzÞT°µ¸^¦³mG(½¯Ó츹ø]zìÕô½íV»ÅÇçJê«sß8 !
²mªgå^ÔÀbá¼,ADÍ·Þ£ÁÉ)^Ù¡HE¦ÊðºoJ@kþß’ªV)ì_KAIIê1ªC8EÁù±LVßÍáðëGöÁPÇöYKN|yRÌ õ¤éó,ÂÆÊ»OÛÔ3üdXÀ¾z¿æ·Syõ÷EºÑ
hÂü0 }1
endstream
endobj
1101 0 obj
>stream
H¬TËÛ@¼òs´ju÷¼4 ±¼X¬nÙ
9ä÷3/=-y}AlÏÔTUW÷©/ª¢iªîýY hÛÓ¹EõîÅ÷?EÕñ$úo»²è_IpµßùMAMÎ
k¢ýÏ¢AV’dS#ë;ÿÜû÷·þñ:¬¶ík¤Zôx5XFPA9%´Ç=¯ÖpÇ«¾È^Î4¿í þÿ» eG¼j`-EI@z½ÿñ÷ó¯ñ, n,%0¹£3=åÕÉsX7(ñ¬ÿþWA¼uí±Z§T£uÁÖÙºlg°Ö^ñEs}yb6«K#’´ÉAf¼0^4Ô«ì×Ì*ªSÑÈÂM0Ó·rôvä;ú¹ØÌúÓþÓçéÍÅOGwÇÏýdqRÇBÊ,´íE
b¢¹Õ’Îôh¬0£ùàìg|5x*¿ï$ãR
]¥oCjÞë8s²ÊÎàtIå¸Ôf|©»åñí)*±c׺Y ;vÂ}*x}${µîÙqÐrOT¹°ÌÏå¬G-ÍØv[ì¬×ª»7ªÂQëePº[À¾M2OoÍ©Qº¨Û`ÃF¾¥Èz6¯ÌÎÐWçM¯Ïy5 [rp
endstream
endobj
1102 0 obj
>stream
HÄK«Û0
÷ùZ&OfFo0Ĺ
îªÞ
K)-]ZúÿW=|ÇvÚÒBcD>G3ç³ÊE¬¬s`òlµ¾íöê0|Ý==÷jw|ÿããwÕ¶ÇçþíE9ÕuçüHjø¤HCE*ßLFyÅäÊÇ?ÈB5|Éh[-Ïw-² È.Ê8!Û72Êìl½N÷]Q/IYpdÔ~Ûgî»ãDIõøBQäbûùÅMö§âïÙNþÉ»¯ÅIÑK>5!¹s³e RûbpÝÃ_}
¸×á]é-¸¹zðܸHÂ
7üß¹)Áé;p®m±È)5Wmú´
®ñéÿSÚvç%ÕøÐˬ@ºIþ®7 ¿é0R1¥º
á½I EÎ[ø
ÉR$gø§ÄÌ©¦%íôÔ5¶S[K!hýè45¨1ÏëMRùX{ÉN(nëaÖ¦uaÍ~ái!Þ aÏ
z~ðlíݾÛ}[:¼ (Ýÿ£V´ÓÛªôTßÀ0uÈ»¹ÑMCn´ÛÞüõÕ¥Dé¸{Qê§ û:o
endstream
endobj
1103 0 obj
>stream
HÌÁjÃ0ï½Í¡,[r!°¦-lÐÓrÛÊ;6öþ§Ù±ÛfmÑÃFIëýýhï³¢mA(Ѿg ÚW1yû
>ïJ 0!
R#ÿÖ[öXò- ùÉ?@ë|zn|ÖþÚúaÖÛS M,6 ÆÅÕéÃrIGWúfm¨T#ô©ßfß_¼Ú4″+¾_¾DUæn)u½Xç{Ñy¨ì¾²He:Ü|®J7£
@ÌÒ°`K²Ð¢ýLiãN»ì
iéÊX«»R>Áä¤ÅTMIjð,(CÒû³0¥ß»KüÎ=bc5-u½Î(IË(b³Äêàëoy=ìT4Eh/qB]Ôc´õÚÊÒþÃá)ôÄj£%Að_ÜCªX°û2hüýEFùÑ$?éüúãé&á´S8û Fqò¥8ÑJNý?p8]*c´úR¤öRúÊH#Î2ß
ñ#À ýûx`
endstream
endobj
1104 0 obj
>stream
H´MÛ0ïýstVF£/!qZhaOõ
˲K
Þú÷wÆVÖ+¥eid!Ï;3ï#Ãø±B@ ÿyrÞ+ëÁSPÑÀø½ªa7~«ÞÝPí?ý|ü]·¿>@·Ð÷Çï£BÔS £b;ÇV’^ke)EÓxKBîzà0~H3üÖøuH6″ùÇÇÀã0?»÷$ë^Bc0Õáú8©·$$ÇP±Ä|ì3Ë ûÆËZdý;«8^*^§¸zª«°)lþÑïËÝvg×è6Öqw.»·îwÉ=¿tÏE§]¹ç¶]:ññâÝügËëCÆ?«0KWö±?%PÜ»$àz´¿!1#°ª»èDàNÊVb§Væ
®Âo_WÎRn3{ì×¥_³hßî*ÙÛ¤o²-½î?{
XXzMpC
ÏÁÛrÈÒLdÍIæg¯ÕþIÎ7ßLÍ3¤¢µëazn´P21dTHµT&üïºc
î«9äò7ÆÌa¹Âoöö¡áffo¸Á÷7M ·6Üù
¶Ö¸;¼0 bÿt¬
endstream
endobj
1105 0 obj
>stream
H´MK1ïþÛCÓÉäkËB» и·*»AñæßwòÕ]ÛMéA[ÒIwwyõ·°þ
d@_
Ú®ÓÖq¬ÿ¨flÞ¿WÛ]Ǫåý×ó’kå®»Ù0T¬m×z@È $¹«£Xè9Ç%ÉÉ
rÈEPvøDÃXÿæó¹¿þµj U
hµ ¾¦¶Ñè-5ôýÖö}ÖóR¡¢Ôl2aíGGå (h!&0r»Á¤ªpþäVªA5oÃÇU[¨¦ÎÕÒ,¢D²ÃDÁýÿÑçáÊÿ΢V3óÇ2cÿ8qPJtÑÎ&Ý18䮩uÑ-ÿÿÀP5¦$¿YØS:ë%]»0¾ó%:¶’û#Îpw²!?ÄG£ùÄ ½ 8]çü5)#ZÄ9ZÆöi©Ñ2 À°Þ± lÐrpPÒQ&`¬hºI°tGNBc}æÂÇ4£círº@¬HZâ×L!YàPFR¬Ó¤’àÁxJ5øJw§ÀþJBÏ!26µK¬jHâÂ~ [lO
endstream
endobj
1106 0 obj
>stream
H¬UMkã0½ûWè,>f$1$q»ÐÓúVB)-=véÿ?U#ɳM`× $èÍyOãî¤@(1½5-H ¥Åô»´ÔhéµyìAÛh ZÏð>Þóô³é¦©@@ÞìµÏwb?½7Ýw¿©mÈ_E4Òq¨:æ5sDçã0åýýÀ`ÁP V¥@ÿ»Ã+ëãøy¼¯&vÀJë5ç`ùÝ=DÓýúxþ#ú¾{8ý
Qb#?ÿÌÅÎÔwò®}«¼Ý)½gêp»1ý.åªÑÕ3ÝÄÑ$$#Ï`i4$lðÒÙ§¥©ªi¿DXT*2ße¥yMº&ÊVR×NJ,ãåd¥ûÃ,mÇd£Ù4ÖuÌ&âÓaû
¡¢o]HfªUÚlÃHtø?qíÜðÈ
¨«±7{ÄkIðå[õ{+KKýÅzG ²[í§¦cÄ;ó9ÃîÖüQ
ïßÚ
Ï1YGùÃî¶Ñ?QâÜeK
wá²ZdnÒºob#¼ØS’TZ¬Ójq»|f3ÿ7r
RËU6ú=¸NÞòß´uòHg!> ØqÐ
endstream
endobj
1107 0 obj
>stream
HÜOkÜ0Åï~½¤ýÅPï&@Nõ-)¥´ôPhÈ_¿IqÌF6Í)!}ïæÔt×]ßUwõåùû:®î·’eY
Ãx÷ÓJ«éW·G@D¯¦ÊqT¨¦ÝCËg·×zív_0Ê^mÒFrhÕô§ëÕnúÝàæ Gó& ÚeQ1ݼ
6(Jlò
}FcO2Éäµ+W£Ó↑OõäçVF6¢l1JÁ»ÓðeÍ7
#tùkßrÁ]ÀP
DSzNé]Ý©ñM53+fHvÃL
Îflg3&£+=ñ+PdQäMÿx?ÍH
-¤_G*¼ÄÏm£!G@Tå,èfÛ
0xå»V&äDõTÃems´Å1òܼ(ÆaϲÅÍó §t&o Ä-*ÆEþëZW*Ö»RþÛµÍ[ÆÙXÇñzq=
NwAïÖp¬±Fx1kÀâÌùð¬Ëjëu½îL¹äú’oë÷v-6¸·fê ùmÐ
endstream
endobj
1108 0 obj
>stream
H¬[kÛ@
ßýóh?d4{Õ.%;ÐBh!ûæâ:NëB¬Thÿ}÷»Ç²++M[Á²ÒÎ9óI Ü}FHDܹ@àî² qý2iW×~/üªÒª¦î[¶¸© Ëo×{Lòêí$é´sç($2ô#|õ5¾bF¯Ü»ã^¦´F©A
H{ÈF0¾P#?ÔQI 5I,ÞYÂË1·rETÌ+þ:Ñ©ø>*âÏÑÉõk¢S6BÕûã1©ØBÍdõ¦ý¬¤=Ϊ5TÞPAÓð >2_°Ó&
Û«/´jýn Ê·f³K!È8Jnÿ²3Ü8
áÖåã»nòq#L>ã&{‘SôàÖ¢¾Ìv:áYBb·ð[à½FÒqöo¨00ê?`pr}|ÓE
¡Ñå
ËòÙS³»_oÐȬiÖ¯Û;XæeÝ4õ¬ò²¬ÀÒ(ÂÿL[ÔÚ
PëVùí÷ÏÍÏÇ-ä×uÝl wñéÃúËn¿nvõþNé=ßWàC#8ëÃÖÔ`qB5Óh 1É»Åà sºWZ
endstream
endobj
1109 0 obj
>stream
hÞj«`à°«Á@À»ô³ÿ0Úÿÿÿý Ã
wD
endstream
endobj
1110 0 obj
>stream
hÞÜ{y`TE¶÷©ª{»; îldé%ÎB’$$H¤³
e$&!ì ¸`AeP ÔNG4 £Ñqyê øfÄeÁmFQô
¹ïW·»Cú¡óÍ÷Ïw/¿:Uçª:UuêTÝØ#¢ZCòÆMÊÍ·¶æ|ÎÀÔæË_e¿u
!2>?§e/5LoÏ]tåÉ÷ß]G4¼
¨æÍnuøW)k:¯Gý¡óÀþ»ú»å´y.»¢½%f.ZÜÜÄÞÓênAýÄìK®h23ëè¿úË.}¯åðz¢ö;Ðß¡¥³[>¾õ^¢¬éh£?1QȶJ¤Þ¦ÀJw]4G3sP
èªõkHL2¹hñeÉKí´z}w5+0:Ùã^b¦I©z0ì@²ØJIDÚ»ÀÀÇÝcPg!¹ºhÇE(?¶ÑNJ£l0=C]4î£2O[éB:Lû(®d/B.ª¤ÈÍìÄ©âJÛéMNKéC:NTCï°h´SE-GEÚ’Hkhv ZáTAÓA¶M¢äGñlæAϵ.§LíöJwÒ,Mk§QÈý¢(VÓMè%í´ I÷³ìrR#mT(mÚBAûé5VÜEt¥úFØ~ZZ÷°xÖ¥Ó>¢’F³ÑÒoh,öS$*Ô]ä tº.¦&HMo²þl°ðjZ¹¶ÜûéKîáÏ#ìðÐh¸É&º³q> ¯Y+dw²=x_e«oÀ¶ZNWÁïÄìÝO{é ÌóxÙ§,ÙfÚþ;è«au¬=-v«yÝ¥Z«}5Hµ°p’=>N±*)6eæpÝAGèUØñæýkú÷]~5_MÓÐ>Ô}ÅNÃiÕÓbZAÓÝXÕgèYú’ûAó°òzzR» sNå°}´’¡íX%?uâ=QF1F1]Ì&²¹l3ÛÆ:ÙìMnàN¾*|âeñ¶2TUµb´G6ôë¢i4+p5fû&÷z^d±,å`DGQÿ>Wâ½æïub³rZ½¶ûx÷?º¿×ÚÈ/»ó°Ä,|Áâ`C[ÀZÙû°|DD
«pBQ&&:±Alÿ%^Q*{·ÔÑjºÇØÔ}Y÷«Zö[Ì#ìÊ lBÃà?sàMa_Þ¥´®¡6ºþrí¢=÷Sô»½F£Ï°Ä°y>z¿^·Ýw;ÛËfϱٻìùòT¼|(/å¼ÏåëðnåGøQþ±HÍbµXwxT¼©¢(wºQ½ßð²1Ó8Ê8Óô§Ó’Î
VnîÆû oÈƪ²Ùh¼± x§àÆêñ6±lÞÕl
û
[Ë~Ë6±ßéïÛnö{ö(ÞÇØA¼¯±cìïìSö%sovóË0Ò
~!Ç’âËãmáKù
¬Ðý¼àGEá9¢I,ÛÅÃâññÂl%W)Q¦*sµÊaåUå
å{Õ®V©óÔê3$ÃÃÃÃ}
§ãxãLãJã_Éhõƽz?¹Ã¬UQ®àÇ°/DºMÁød±HÜ þ[ÃN
{µùb¡v¨æÿÙTþKvµXÌ¡ëIc{ø»üÿHeù’,S¹=Æ
nÐãêXeú1ù*ÖÅkÅZíT¬î`ÇÔüUr(Çy:]½ßJ¯ðù|#Õ*CÔïi>æý÷êï|(þ¢ì
ÅN²mØ%_ÂØDÜ3ÌF’Øja¿#/{ýucûÙXÞ«åãf6Ù!ádáT’mdéñáÎ(ñßt,¾zºé2ì1
ÑäÏ,èÄûSÝOȾ¡nÝ%²i»åÑþ2co|·®¥|:Ü@yüVZ©a³÷/BüäÔÉP.@´m«q^ÄñTÄÂôú/ÄÿõkØçt9s`guQ¦»%×+UL¿ñ΢(ÝA7ö«¦q,Hqtï¿MàÌyý’R 쫧»lXí@d^wt¹è
/3N«`óHìóñÊ(DÞmÚp>Ψ±8_¤ùÚ-Tµ¨Õ6Rv6æÒ$íÄßÒzµOU=ÊÄØÙ³8þÊ6″n¢·Ü,>ÅóFªSò:bg©v½öÅb>R1C3q~@Òç·Q¢
º/æíZµhÁ u&h÷kvNó´E¼OÐn£Ø³lênø.y˧Lö¼ dDqÑðaCäÎËíîNs¥:v[JrRâø¸þÑQVK¤¹_DxÉhPÁeW¹ª¾ôFî5*G]M`4õb4ú`U«ãs4êjs5½ÐÓGÓÐôöh2«£Jr²U.ïP¥ËÑÉê’Ô»¿©ÒUçðÐóéù-zÞ¼Ó
ªyktTùªWÌk«j¬Dsíá®Ùá9ÙÔlr¾xWK;Éô¯*nçd2Ã(_¢«²Ê7ÀU)-ð wUÓ,ßø µUINg]N¶U4»fúÈUî³xtªÐ»ñ*|F½Ç|9ÚèhÏîj»¾ÓJ3=ýf¹f5M¯õ¦:ÙGýVúâ¯ú álGWÔ®ï-MmU ó²ØÖ¶ÞáÛ5¡¶·Ô)Óº:´áãîêƶjt|=¦°f}ñuuµ>¶:ä8ä£íªÆ_«Ü5¯mA#&±ÍG¯tú½´ãXåhërúJuMÉí1Ô6ñÊ^Çs%9ÙíÖ¨À´¶GZ~æÞÙ=2=§«ËÍÄyeÒ»×h¸ÏÑì%µ.i¸Lf§¶æáPÃSÇPË7ë1ßVÑØf-ß*ëûT·Õåhû°þ®Ëi
rnë×$³ÒKz
òPÞçñøb¬ÀÂÆz¹0′{E’÷¹Z¬LÇÜ6ÕçbòN¹¼;½4ß µ²f&ùÉë©óñF)é
Ib§Hɤ§z£~üÉïX)½çÅ׿j^±ÅýijòI® õµª¶ÆàÜÖL>§ïs, Àû7fj´®7±¾V2ðOuW»ªæ7ÂV¾þµ»×r
Источник
Задача 3. Расчёт статически неопределимого ступенчатого бруса — КиберПедия
При растяжение (сжатие)
Для статически неопределимого бруса с жёстко защемлёнными концами, нагруженного продольной нагрузкой как показано на схеме к задаче 3 необходимо:
1. Построить эпюры продольных сил N, нормальных напряжений и перемещений ;
2. Подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок,
Необходимые данные для решения задачи взять из таблицы 1.3.
Схемы к задаче 3
Схемы к задаче 3
Схемы к задаче 3
Таблица 1.3
| Вариант | Усилия | Длины участков | ||
| Р, кН | q,кН/м | l1, м | l2, м | l3, м |
| 27 | 12 | 2 | 0,5 | |
| 35 | 24 | 1,2 | 1,9 | 0,8 |
| 53 | 46 | 1,3 | 1,8 | 1 |
| 29 | 10 | 1,4 | 1,7 | 1,1 |
| 37 | 22 | 1,5 | 1,2 | 1,2 |
| 45 | 32 | 1,6 | 1,4 | 2 |
| 10 | 30 | 1,7 | 1 | 1,8 |
| 15 | 18 | 1,8 | 1,1 | 1,5 |
| 25 | 20 | 1,9 | 1,2 | 1,2 |
| 50 | 44 | 2 | 0,8 | 1 |
Пример решения задачи 3
Для ступенчатого бруса (см. рис. 1.5а) построить эпюры продольных сил N, нормальных напряжений и перемещений ; подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок если Р1=3Р; Р2=2Р.
Решение
Задача один раз статически неопределима в силу плоской системы сил, действующих по одной прямой, для которой как известно можно составить только одно уравнение равновесия:
,
в котором два неизвестных: и .
Отбросим правую опору, заменив её действие на брус реакцией .
Перемещение сечения в точке В равно нулю, т.к. это сечение жёстко заделано. Используя принцип независимости действия сил, получим уравнение совместности деформаций:
Распишем эти деформации по закону Гука:
,
отсюда, после сокращения на а и EF, кН.
Рис. 1.5 Расчётная схема и эпюры для примера решения задачи 3
В соответствии с расчётной схемой рис. 1.5б аналитические зависимости N, и будут следующими:
Участок 1
кН ; ; .
Подставим в уравнение для перемещения два крайних значения , после подстановки будем иметь:
.
Участок 2
кН; ; .
Подставляя пределы получим:
.
Участок 3
кН; ; .
Подставляя пределы получим:
.
На основании данных аналитических зависимостей строим эпюры N, и (рис. 1.5 в, г,д).
Построение эпюры перемещений может служить проверкой правильности решения задачи. Перемещение на участке 1 при z1=0 равно нулю, перемещение на участке 3 при z=a также должно равняться нулю, т.к. эти два сечения соответствуют жёсткому закреплению бруса, перемещения которых невозможны.
2. На эпюре нормальных напряжений найдём максимальное напряжение: .
Для определения площади поперечного сечения воспользуемся условием прочности по нормальным напряжениям:
.
Приравняв максимальное нормальное напряжение к допускаемому, определим площадь поперечного сечения F:
.
Таким образом, на участке 1 площадь поперечного сечения должна быть , а на участке 2 в два раза больше, т.е. .
Плоский изгиб
Изгиб называется плоским, если плоскость действия изгибающей нагрузки проходит через главную центральную ось инерции сечения.
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы изгиб называется поперечным.
Брус, работающий при изгибе, называется балкой.
Построение эпюр поперечной силы Qyи изгибающего момента Mx является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Qy и Mx определяется опасное сечение, т.е. сечение в котором может произойти разрушение.
Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения .
В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила .
Между поперечной силой и изгибающим моментом существует следующая зависимость:
,
то есть первая производная от изгибающего момента по длине участка равна поперечной силе.
Это соотношение в общем виде было получено Журавским и носит название теоремы Журавского.
На основании теоремы Журавского могу быть сформулированы правила проверки эпюр:
1. В точке приложения сосредоточенной силы на эпюре Qy должен быть скачок, равный по величине и знаку приложенной силе.
2. В точке приложения сосредоточенного момента на эпюре Mxдолжен быть скачок, равный по величине и по знаку приложенному моменту.
3. На участке, где приложена распределенная нагрузка, эпюра Qy является наклонной прямой (наклон по направлению действия нагрузки), а эпюра Mx — параболой, выпуклость которой направлена навстречу распределенной нагрузке.
4. На участках, где Qy > 0, Mx возрастает, на участках, где Qy< 0, Mx убывает, если Qy = 0 (эпюра пересекает нулевую линию), то эпюра Мx имеет экстремум.
5. В тех точках, где на эпюре Qy имеется скачок, на эпюре Мx будет излом.
6. Чем больше по модулю величина Qy , тем круче изменяется эпюра Мx.
7. На свободных концах балки изгибающий момент равен нулю.
Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении
.
Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений
Источник
Тема. Центральное растяжение (сжатие)

ЗНАЕТЕ ЛИ ВЫ?
Задача № 1 Расчет бруса на растяжение (сжатие).
Общие сведения
Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила. Продольная сила в поперечном сечении бруса численно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса).
Растягивающие (направленные от сечения) продольные силы считаются положительными, а сжимающие (направленные к сечению) – отрицательными.
При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле
где N − продольная сила; F − площадь поперечного сечения.
Для наглядного изображения распределения вдоль оси бруса
продольных сил и нормальных напряжений строят графики, называемые эпюрами.
Деформацией при растяжении участка бруса является его удлинение. Абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине участка бруса и обратно пропорционально
жесткости сечения бруса
где EF − жесткость сечения.
Коэффициент E характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия и называется модулем упругости первого рода; для стали
E = (1,96…2,16)·105Па.
1.2 Пример.Построить эпюры продольных сил, нормальных
напряжений и перемещений поперечных сечений по длине ступенчатого
бруса (рис. 1). Материал бруса – сталь Ст.3; E = 2 ⋅105МПа; P = 60 кН;
F1 = 5 см2; F2= 12 см2; a = 1м.
Решение. Разбиваем брус на участки 1(АВ), 2(ВС) и 3(CD).
Применяя метод сечений, рассматриваем равновесие левой части, отбрасывая при этом отсеченную правую часть
Для участка 1 N1= P= 60кН;
Для участка 2 N2= P= 60кН;
Для участка 3 N3= P+2P=3P=180кН.
Эпюра, показывающая, как меняется N по длине бруса, изображена на рис. 1.
Для построения эпюры нормальных напряжений, находим напряжения на каждом участке:
Рис.1.1
Эпюру перемещений строим, начиная от защемленного конца D. Перемещение поперечного сечения, где проложена сила 2P (точка С), равное удлинению участка CD.
Перемещение сечения В относительно сечения С равно удлинению участка ВС.
Абсолютное перемещение сечения В:
ΔB = ΔC + ΔBC = 0,75 + 0,25 =1,0мм .
Перемещение сечения А относительно В, равное удлинению
участка АВ:
Абсолютное перемещение сечения А:
Δ A = ΔB+ Δ AB = 1,0 + 1,2 = 2,2мм .
Построенная по полученным данным эпюра перемещений
показана на рис. 1.
1.3 Задание 1. Вариант 1. Построить эпюры продольных сил, нормальных напряжений и перемещений поперечных сечений по длине ступенчатого бруса по данным одной из схем, приведенных на рисунках 1.2.
Вариант 1
Исходные данные: P = 50 кН; F = 5 см2; l = 1 м.
Рис.1.2
Вариант 2
Для стального бруса, нагруженного продольными силами Р, с учетом собственного веса (рис.1.3) требуется:
1. Определить внутренние силы, напряжения и перемещения по длине бруса.
2. Построить эпюры нормальных сил, напряжений и перемещений по длине бруса.
3. Указать положение наиболее опасного сечения и величину нормального напряжения в этом сечении.
Принять, что материал бруса имеет плотность γ = 7,8 г/см3 и модуль продольной упругости Е = 2•105 МПа.
Таблица 1.1 – Исходные данные
| № варианта | Р, кН | F, м2 | a, м | b, м | c, м |
| 1,2 | 16•10 — 4 | 1,1 | 1,2 | 1,3 | |
| 1,9 | 13•10 — 4 | 1,4 | 1,7 | 1,5 | |
| 1,7 | 11•10 — 4 | 1,7 | 1,5 | 1,7 | |
| 1,3 | 15•10 — 4 | 2,0 | 1,9 | 1,8 | |
| 1,5 | 17•10 — 4 | 2,3 | 2,2 | 2,0 | |
| 2,0 | 19•10 — 4 | 2,6 | 2,5 | 2,4 | |
| 1,1 | 18•10 — 4 | 2,9 | 2,8 | 2,7 | |
| 1,6 | 14•10 — 4 | 1,5 | 1,6 | 1,6 | |
| 1,8 | 12•10 — 4 | 1,8 | 1,8 | 1,9 | |
| 2,2 | 10•10 — 4 | 1,2 | 1,3 | 1,4 |
Рис. 1.3
Литература:
1. Волков А. Н. Сопротивление материалов. — М.: КолосС, 2004. —
С.18…19.
2. Кривошапко С. Н. Сопротивление материалов: лекции, семинары, расчетно-графические работы. — М.: Издательство Юрайт, 2013. — С.187…194.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3
Источник