Для заданного бруса построить эпюры нормальных сил

Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.

Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.

Но всему свое время. Сначала немного о терминах.

Основные понятия

Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.

Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.

Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.

В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).

Что такое эпюра продольных сил

Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.

Как построить эпюру продольных сил

Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая. 

Сопротивление рассчитывается по формуле:

где:

• Fl – действующие на участке l силы (Н);

• ql – распределенные нагрузки (Н/м).

Порядок построения:

1. Рисуется схема балки и механизмов закрепления;

2. Производится разделение на участки;

3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:

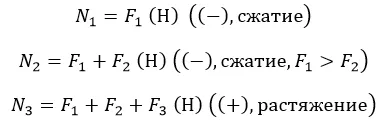
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;

4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.

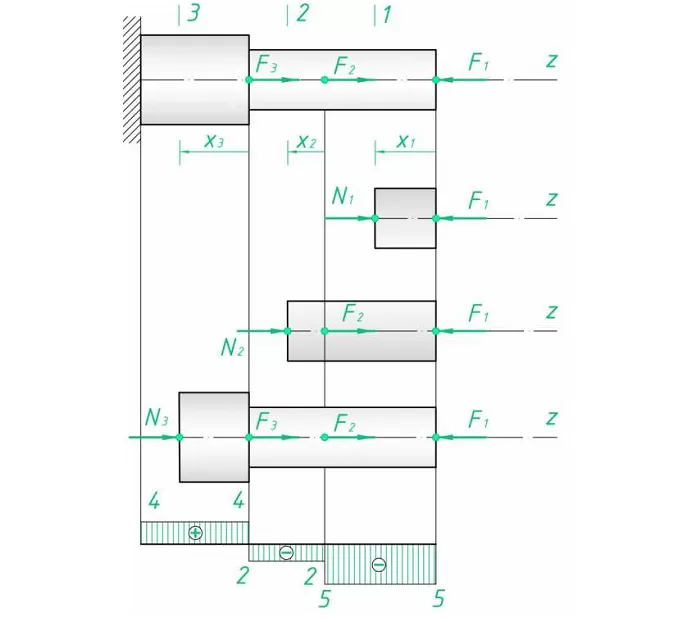
Рис. 1. Эпюра продольных сил

Рассмотрим случай:

F1 = 5 (кН);

F2 = 3 (кН);

F3 = 6 (кН).

Вычислим:

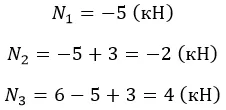
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.

Пример построения эпюр и решения задач

Построить эпюру сил для следующего случая (рис. 2):

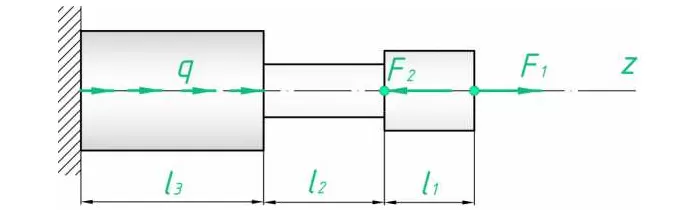
Рис. 2

Дано:

Решение.

Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:

Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.

Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.

По полученным данным строим эпюру (рис. 3).

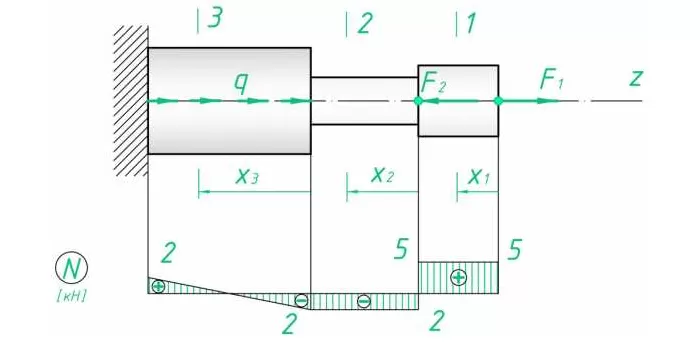
Рис. 3

Заключение

Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.

В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.

Тема: Решение задач на построение эпюр нормальных сил, нормальных напряжений, перемещений сечений бруса.

Ознакомиться с примером построения эпюр продольных сил, напряжений и перемещений.

Задача 1.Двухступенчатый стальной брус нагружен силами F1=30 кН F2=40 кН.

Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=1,5см2;А 2=2см2.

Решение.

Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.

Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.

Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Разбиваем брус на участки.

Определяем ординаты эпюры N на участках бруса:

N1= — F1= -30кН

N2= — F2= -30кН

N3= -F1+F2= -30+40=10 кН

Строим эпюру продольных сил

Вычисляем ординаты эпюры нормальных напряжений

σ1 = = = –200МПа

σ2 = = = –150МПа

σ 3= = =50МПа

Строим эпюры нормальных напряжений.

4. Проверяем прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Выбираем максимальное по модулю расчетное напряжение. IσmaxI = 200 МПа

Подставляем в условие прочности IσmaxI ≤ [σ]

200 МПа ≤ 160 МПа. Делаем вывод, что прочность не обеспечена.

5. Определяем перемещение свободного конца бруса Е = 2∙10 5 МПа.

∆l=∆l1+∆l2+∆l3

∆l1= = = – 0,5мм

∆l2= = = – 0,225мм

∆l3= = = 0,05мм

∆l= — 0,5 – 0,225 + 0,05 = – 0,675мм

Брус укоротился на 0,675мм

1. Задание: Решить задачи

Двухступенчатый стальной брус нагружен силами F1, F2.

Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=5 см2;А 2 =10 см2. Длина l = 0,5 м. Первая команда F1= 50 кН, F2 = 30 кН. Вторая команда F1= 30 кН, F2 = 50 кН.

F1

l l l

l l l

Разбить брус на участки. Пронумеровать эти участки.

Найти величину продольной силы на первом участке.

Найти величину продольной силы на втором участке.

Найти величину продольной силы на третьем участке.

Построить эпюру для продольной силы.

Найти величину нормального напряжения на первом участке.

Найти величину нормального напряжения на втором участке.

Найти величину нормального напряжения на третьем участке.

Построить эпюру для нормального напряжения.

Проверить прочность бруса. Допускаемое напряжение [σ] = 160 МПа.

Определить перемещение свободного конца бруса.

Задание 2

Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Задание 3

Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

 Литература
В.П. Олофинская «Техническая механика» курс лекций с вариантами практических и тестовых заданий.
Лекции по теме (конспекты).

Построение эпюр нормальных сил и напряжений для брусьев в статически определимых задачах

Задача 1.1.1. Построить эпюры нормальных сил и нормальных напряжений для бруса, изображенного на рис. 1.1.1. Собственный вес бруса в расчете не учитывать.

Решение. Для определения внутренних усилий разбиваем прямолинейный брус
на участки. Границами участков являются точки продольной оси, соответствующие
изменению площади поперечного сечения и точкам приложения сосредоточенных
сил. Из рассмотрения рис. 1.1.1, а определяем, что брус необходимо разбить
на четыре участка.

Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим
нормальной силой N1 (рис. 1.1.1, б). Запишем уравнение равновесия, проектируя
силы на ось бруса:

откуда N1 = F.

Очевидно, что на всем первом участке () нормальная сила N1 постоянна по величине. Откладываем
в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис.
1.1.1, е).

Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее
действие нормальной силой N2 (рис. 1.1.1, в). Проектируем все силы на ось
бруса:

откуда N2 = –F.

Рис. 1.1.1

Аналогично находим нормальные силы в сечении III – III (рис. 1.1.1, г):

откуда N3 = –F

и в сечении IV – IV (рис. 1.1.1, д):

откуда N4 = 0.

Откладывая в масштабе значения нормальных сил N2, N3, N4 в пределах соответствующих
участков, получаем эпюру нормальных сил (рис.1.1.1,е). Полученную таким путем
эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая
такая линия в принятом масштабе дает величину нормальной силы в соответствующем
поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка
– растяжение, а знак «минус» – сжатие.

Для построения эпюры нормальных напряжений воспользуемся формулой (1.2) для каждого
участка:

Эпюра нормальных напряжений (рис. 1.1.1, ж) показывает, что наибольшего
значения нормальные напряжения достигают в пределах третьего участка (участок
III).

Задача 1.1.2. Построить эпюры нормальных сил и нормальных напряжений для
бруса, изображенного на рис.1.1.2, а. Принять a = 0,4 м; площадь поперечного
сечения бруса на участках III и IV А = 20 см2; сосредоточенная сила F = 0,5
кН, собственный вес = 0,0078 кг/см3 = 76,44 кН/м3.

Решение. Для определения внутренних усилий разбиваем брус с прямолинейной
осью на четыре участка. Проводим сечение I – I (рис. 1.1.2, а) и отбрасываем
верхнюю часть бруса, заменяя действие отброшенной части нормальной силой N1
(рис. 1.1.2, б). Так как сечение I –I может быть проведено в любом месте участка
I, то длина оставшейся части участка будет переменной величиной, и поэтому
обозначим ее через x (рис. 1.1.2, б), причем . Запишем уравнение равновесия, проектируя
силы, действующие на оставшуюся часть бруса, на направление оси бруса:

откуда

Рис. 1.1.2

Через обозначен собственный вес оставшейся части бруса первого
участка, в пределах которого площадь поперечного сечения равна 2А, а длина
оставшейся части обозначена через x. Подставим численные значения в полученную
формулу:

.

Записанное выражение показывает, что эпюра нормальных сил в пределах первого
участка представляет собой наклонную прямую линию. Для построения этой прямой
определим значение нормальной силы N1 в начале первого участка (x = 0): N1(x
= 0) = 500 Н и в конце первого участка (x = a= = 0,5 м): N1 (х = 0,5 м) =

Полученные значения откладываем в масштабе в соответствующих точках эпюры
нормальных сил (рис. 1.1.2, е). Найденные точки соединяем прямой линией, затем
штрихуем первый участок эпюры прямыми линиями, перпендикулярными к оси бруса.

Проводим сечение II – II и повторяем порядок расчета, описанный выше для
сечения I – I. Переменная величина х участка II – II будет изменяться в пределах
. Составим уравнение равновесия
(рис. 1.1.2, в)

откуда

где – собственный вес части
бруса, расположенного ниже сечения II – II. Окончательно имеем

Определяем значение нормальной силы N2 в начале второго участка (х= 0,5
м): и в конце этого же участка (х = хmax = 1 м):

Полученные значения N2 откладываем в масштабе в начале и в конце второго
участка (рис. 1.1.2, е).

Проводим сечение III – III и для оставшейся части бруса составляем уравнение
равновесия (рис. 1.1.2, г)

откуда где – собственный вес оставшейся части бруса третьего участка;
– собственный вес первого
и второго участков.

Тогда для участка

где нормальная сила N3 в начале третьего участка будет N3(х=0) = –194,2
Н; а в конце третьего участка получаем N3 (х = a = 0,5 м) = –117,8 Н. Найденные
значения N3 переносим на эпюру нормальных сил.

И наконец, рассматривая равновесие оставшейся части бруса, после проведения
сечения IV – IV получаем (рис. 1.1.2, д)

откуда где = 305,76 Н – собственный вес участков I – I и II – II,
152,88х – собственный вес
третьего и оставшейся части четвертого участков.

В этом случае имеем

т.е. в начале четвертого участка N4 (х = 0,5 м) = 382,2 Н, а в конце этого
же участка N4 (х = 1 м) = 458,64 Н. Вычисленные значения N4 откладываем в
масштабе на эпюре нормальных сил (рис. 1.1.2, е).

Эпюра нормальных сил показывает, что первый и четвертый участок подвержены
растяжению, а второй и третий – сжатию.

Для вычисления значений нормальных напряжений и построения эпюры нормальных напряжений
используем формулу (1.2):

Эпюра нормальных напряжений
показывает, что самое большое нормальное напряжение возникает в сечении, проходящем
через точку Л четвертого участка (рис. 1.1.2, ж), т.е. на опоре.

В брусе сечение проводят перпендикулярно его оси. Такое
сечение называют поперечным.

Величины внутренних усилий определяются с применением метода
сечений, суть которого заключается в следующем. Если при действии внешних сил
тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с
приходящимися на нее внешними и внутренними усилиями также находится в
равновесии, следовательно, к ней применимы уравнения равновесия.

Рассмотрим тело, имеющее форму бруса (рис. 1.4, а).

Пусть к нему приложена некоторая система внешних сил Р1, Р2,
Р3,…, Рn , удовлетворяющая условиям равновесия, т.е. при действии указанных
внешних сил тело находится в состоянии равновесия.

Если рассечь брус сечением А на две части и правую
отбросить, то, т.к. связи между частями тела устранены, необходимо действие
правой (отброшенной) части на левую заменить некоей системой внутренних сил (PА
), действующей в сечении А (рис. 1.4, б).

Рис. 1.4

Обозначая через и суммы внешних сил, приложенных соответственно,
к левой и правой частям бруса (относительно сечения А), и учитывая, что

                      (1.1)

для отсеченных частей бруса получим следующие очевидные соотношения:

; .           (1.2)

Последние соотношения показывают, что равнодействующая
внутренних сил РА в сечении А может определяться с равным успехом из условий
равновесия либо левой, либо правой частей рассеченного тела. В этом суть метода
сечений.

Внутренние усилия должны быть так распределены по сечению,
чтобы деформированные поверхности сечения А при совмещении правой и левой
частей тела в точности совпадали. Это требование в механике твердого
деформируемого тела носит название условия неразрывности деформаций.

Эпюра продольных сил N — это график, показывающий, как изменяется продольная сила по длине бруса.

Пример 1. Построить эпюру продольных сил для бруса, нагруженного осевыми силами (рис. 2.2.5).

Для построения эпюры продольных сил проводим прямую, параллельную продольной оси бруса (базовая линия). Значение нормальных сил откладывают в выбранном масштабе и с учетом знаков (положительные силы откладываем вправо от базовой линии, а отрицательные — влево) на уровне соответствующего участка. Участком считается расстояние от силы до силы, т.е. границами участков являются сечения, в которых приложены внешние силы. В нашем примере у бруса три участка: АВ, ВС и CD.

Штриховка эпюр означает величину продольной силы в любом сечении бруса, проводится перпендикулярно продольной оси стержня.

Рис. 2.2.5

Построение эпюр начинаем от свободного конца.

Применяя метод сечений, мысленно рассекаем брус на участке АВ (сечение I—I) и отбрасываем его верхнюю часть. Рассмотрим равновесие оставшейся нижней части: ‘ZFz = F] — У, = 0;

Nx = Fv Поскольку Fx направлена от сечения, то N{ = Fx = 25 Н. На всем участке АВ продольная сила положительна (так как участок растягивается). Откладываем ее в масштабе вправо от базовой линии. Далее проводим сечение II—II на участке ВС, мысленно отбрасываем верхнюю часть бруса и рассматриваем равновесие нижней части:

Продольная сила N2 отрицательная и направлена к сечению. Аналогично определяем значение продольной силы в сечении III—III на участке CD:

Продольная сила N3 направлена от сечения, т.е. является растягивающей. Итак, продольная сила А в любом сечении равна алгебраической сумме продольных сил, действующих по одну сторону от сечения.

Пример 2. Для бруса со ступенчато-переменным сечением построить эпюры продольных сил и нормальных напряжений (рис. 2.2.6).

Эпюра нормальных напряжений а — это график, показывающий, как изменяется напряжение по длине стержня. Правило знаков такое же, как у продольной силы: напряжение положительное — растяжение, напряжение отрицательное — сжатие.

Вопрос об определении нормальных напряжений связан с расчетом бруса на прочность.

При построении эпюры продольных сил участка считается расстояние от силы до силы (в нашем примере четыре участка: АВ, BD, DK, KL).

гг „ (

При построении эпюры нормальных напряжении I с = — I

участком является либо расстояние между силами, либо расстояние между силами и тем местом, где изменяется площадь поперечного сечения (в нашем примере шесть участков: АВ, ВС, CD, DE, ЕК, KL).

Для построения эпюры продольных сил мысленно рассекаем участок АВ по сечению I—I. Верхнюю часть отбрасываем и рассматриваем равновесие нижней части:

F{ и Nx направлены к сечению, т.е. участок АВ сжимается.

Рис. 2.2.6

На участке ВС в сечении II—II продольная сила N2 равна алгебраической сумме внешних продольных сил, лежащих ниже этого сечения, N2 = — F{ + F2 = —10 + 15 = 5 Н. На участке CD для эпюры продольных сил никаких изменений не произошло: алгебраическая сумма сил осталась та же: N3 = N2 = 5 Н.

Рассекаем участок DE. Продольная сила N4 равна алгебраической сумме сил —Fx + F2 — F3 = —10 + 15 — 30 = -25 Н. На участке ЕК продольная сила N будет такая же, как на участке DE, т.е. существует только перепад сечения, а сила не приложена, N5 = N4 = — 5 Н.

На участке KL в сечении VI—VI продольная сила 7^ = —10+15 — — 30 + 45 = 20 Н.

Все значения продольных сил Nоткладываем на эпюре.

Скачок на эпюре N находится в том сечении, где приложена сосредоточенная сила, и происходит на величину и в направлении этой силы. Так, в сечении, где приложена сила F{, — скачок от нуля на 10 Н в отрицательную сторону. В том сечении, где действует сила Е2 — скачок в положительную сторону на 15 Н, в результате получим N2 = 5 Н. В сечении, где приложена сила Fv — скачок в отрицательную сторону на величину силы Е3 = —30 Н, в результате на участках DE и ЕК имеем N = —25 Н. Последний скачок в сечении, где действует сила Е4, в положительную сторону на 45 Н, и jV6 = 20 Н. При построении эпюры нормальных напряжений надо учитывать, на какой площади поперечного сечения действует данная продольная сила.

Тогда:

По полученным данным строим эпюру нормальных напряжений а.

Пример 3. Стержень стоит на плоскости (рис. 2.2.7). Построить для данного стержня эпюры продольных сил N и нормальных напряжений а.

1. Рассчитаем сначала числовые значения продольных сил.

2. Определим направление этих сил.

Если продольная сила в сечении направлена к сечению, то происходит сжатие, если от сечения — растяжение. Разбиваем стержень на четыре участка: А В, ВС, CD, DE. Эпюру продольных сил N начинаем строить с участка АВ. Мысленно рассекаем этот участок сечением I—I, отбросив нижнюю часть, и рассматриваем равновесие верхней, оставшейся части. Внешняя сила F{ направлена к сечению (сжимающая), внутренняя сила N направлена

Рис. 2.2.7

также к сечению (сжимающая). Из условия равновесия XjF = О, —Fx + Nx = 0 определим Nx = F], откуда следует, что направление силы N{ выбрано верно, т.е. N] — отрицательная. Продольная сила на участке ВС в сечении II—II N2 = —F{, так как до этого сечения действует только сжимающая сила Fv Участок CD мысленно рассекаем сечением III—III и видим, что по одну сторону от сечения (выше этого сечения) действуют две силы: —F{ + F2 = N3, сила N3 растягивающая. На участке DE N4 = N3, так как по одну сторону от сечения IV—IV действуют эти же две силы — Fx + F2 = = N4, N4 = N3. По полученным данным строим эпюру продольных сил N.

Рассчитаем теперь значение нормальных напряжений:

По полученным данным строим эпюру нормальных напряжений о.