Как построить эпюру бруса
Построение эпюр продольных сил — формулы, условия и примеры решения задач
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
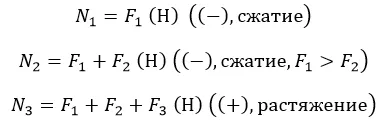
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
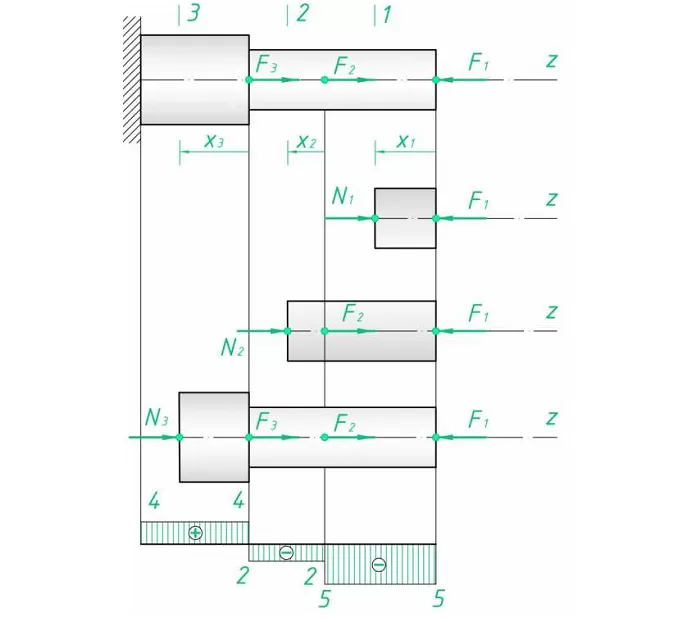
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
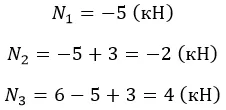
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
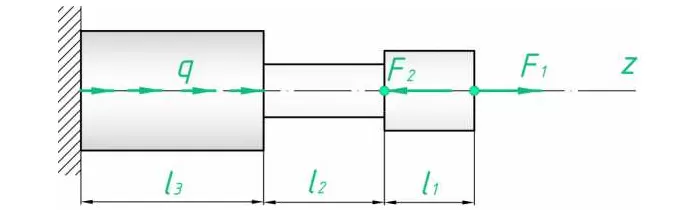
Рис. 2
Дано:
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
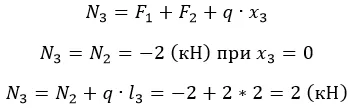
По полученным данным строим эпюру (рис. 3).
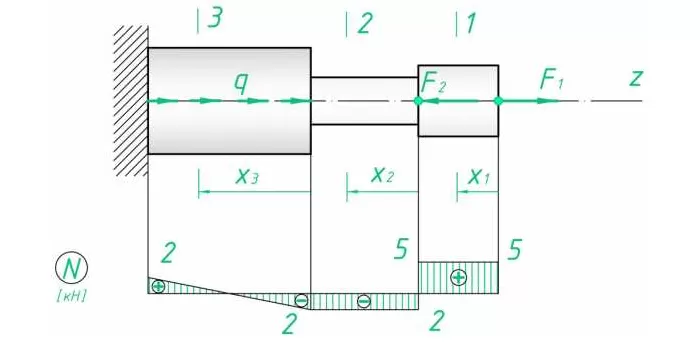
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
ЭПЮРЫ ПРОДОЛЬНЫХ СИЛ N И НОРМАЛЬНЫХ НАПРЯЖЕНИЙ σ
Эпюра продольных сил N — это график, показывающий, как изменяется продольная сила по длине бруса.
Пример 1. Построить эпюру продольных сил для бруса, нагруженного осевыми силами (рис. 2.2.5).
Для построения эпюры продольных сил проводим прямую, параллельную продольной оси бруса (базовая линия). Значение нормальных сил откладывают в выбранном масштабе и с учетом знаков (положительные силы откладываем вправо от базовой линии, а отрицательные — влево) на уровне соответствующего участка. Участком считается расстояние от силы до силы, т.е. границами участков являются сечения, в которых приложены внешние силы. В нашем примере у бруса три участка: АВ, ВС и CD.
Штриховка эпюр означает величину продольной силы в любом сечении бруса, проводится перпендикулярно продольной оси стержня.
Рис. 2.2.5
Построение эпюр начинаем от свободного конца.
Применяя метод сечений, мысленно рассекаем брус на участке АВ (сечение I—I) и отбрасываем его верхнюю часть. Рассмотрим равновесие оставшейся нижней части: ‘ZFz = F] — У, = 0;
Nx = Fv Поскольку Fx направлена от сечения, то N{ = Fx = 25 Н. На всем участке АВ продольная сила положительна (так как участок растягивается). Откладываем ее в масштабе вправо от базовой линии. Далее проводим сечение II—II на участке ВС, мысленно отбрасываем верхнюю часть бруса и рассматриваем равновесие нижней части:
Продольная сила N2 отрицательная и направлена к сечению. Аналогично определяем значение продольной силы в сечении III—III на участке CD:
Продольная сила N3 направлена от сечения, т.е. является растягивающей. Итак, продольная сила А в любом сечении равна алгебраической сумме продольных сил, действующих по одну сторону от сечения.
Пример 2. Для бруса со ступенчато-переменным сечением построить эпюры продольных сил и нормальных напряжений (рис. 2.2.6).
Эпюра нормальных напряжений а — это график, показывающий, как изменяется напряжение по длине стержня. Правило знаков такое же, как у продольной силы: напряжение положительное — растяжение, напряжение отрицательное — сжатие.
Вопрос об определении нормальных напряжений связан с расчетом бруса на прочность.
При построении эпюры продольных сил участка считается расстояние от силы до силы (в нашем примере четыре участка: АВ, BD, DK, KL).
гг „ (
При построении эпюры нормальных напряжении I с = — I
участком является либо расстояние между силами, либо расстояние между силами и тем местом, где изменяется площадь поперечного сечения (в нашем примере шесть участков: АВ, ВС, CD, DE, ЕК, KL).
Для построения эпюры продольных сил мысленно рассекаем участок АВ по сечению I—I. Верхнюю часть отбрасываем и рассматриваем равновесие нижней части:
F{ и Nx направлены к сечению, т.е. участок АВ сжимается.
Рис. 2.2.6
На участке ВС в сечении II—II продольная сила N2 равна алгебраической сумме внешних продольных сил, лежащих ниже этого сечения, N2 = — F{ + F2 = —10 + 15 = 5 Н. На участке CD для эпюры продольных сил никаких изменений не произошло: алгебраическая сумма сил осталась та же: N3 = N2 = 5 Н.
Рассекаем участок DE. Продольная сила N4 равна алгебраической сумме сил —Fx + F2 — F3 = —10 + 15 — 30 = -25 Н. На участке ЕК продольная сила N будет такая же, как на участке DE, т.е. существует только перепад сечения, а сила не приложена, N5 = N4 = — 5 Н.
На участке KL в сечении VI—VI продольная сила 7^ = —10+15 — — 30 + 45 = 20 Н.
Все значения продольных сил Nоткладываем на эпюре.
Скачок на эпюре N находится в том сечении, где приложена сосредоточенная сила, и происходит на величину и в направлении этой силы. Так, в сечении, где приложена сила F{, — скачок от нуля на 10 Н в отрицательную сторону. В том сечении, где действует сила Е2 — скачок в положительную сторону на 15 Н, в результате получим N2 = 5 Н. В сечении, где приложена сила Fv — скачок в отрицательную сторону на величину силы Е3 = —30 Н, в результате на участках DE и ЕК имеем N = —25 Н. Последний скачок в сечении, где действует сила Е4, в положительную сторону на 45 Н, и jV6 = 20 Н. При построении эпюры нормальных напряжений надо учитывать, на какой площади поперечного сечения действует данная продольная сила.
Тогда:
По полученным данным строим эпюру нормальных напряжений а.
Пример 3. Стержень стоит на плоскости (рис. 2.2.7). Построить для данного стержня эпюры продольных сил N и нормальных напряжений а.
1. Рассчитаем сначала числовые значения продольных сил.
2. Определим направление этих сил.
Если продольная сила в сечении направлена к сечению, то происходит сжатие, если от сечения — растяжение. Разбиваем стержень на четыре участка: А В, ВС, CD, DE. Эпюру продольных сил N начинаем строить с участка АВ. Мысленно рассекаем этот участок сечением I—I, отбросив нижнюю часть, и рассматриваем равновесие верхней, оставшейся части. Внешняя сила F{ направлена к сечению (сжимающая), внутренняя сила N направлена
Рис. 2.2.7
также к сечению (сжимающая). Из условия равновесия XjF = О, —Fx + Nx = 0 определим Nx = F], откуда следует, что направление силы N{ выбрано верно, т.е. N] — отрицательная. Продольная сила на участке ВС в сечении II—II N2 = —F{, так как до этого сечения действует только сжимающая сила Fv Участок CD мысленно рассекаем сечением III—III и видим, что по одну сторону от сечения (выше этого сечения) действуют две силы: —F{ + F2 = N3, сила N3 растягивающая. На участке DE N4 = N3, так как по одну сторону от сечения IV—IV действуют эти же две силы — Fx + F2 = = N4, N4 = N3. По полученным данным строим эпюру продольных сил N.
Рассчитаем теперь значение нормальных напряжений:
По полученным данным строим эпюру нормальных напряжений о.
Источник
Примеры построения эпюры продольных сил
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а).
Делим брус на участки нагружения.
Участком нагружения считают часть бруса между внешними силами.
Тема 2.2. Растяжение и сжатие 177
На представленном рисунке 3 участка нагружения. Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Участок 1: ∑ Fz = 0; —3F + N 1 = 0; N 1 = 3F. Продольная сила положительна, участок 1 растянут.
Участок 2: ∑ Fz = 0; -3F + 2F + N 2 = 0; N 2 = F . Продольная сила положительна, участок 2 растянут.
Участок 3: ∑ Fz= 0; -3F + 2F + 5F — N3 = 0; N 3 = 4F . Продольная сила отрицательна, участок 3 сжат. Полученное значение N 3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.26).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz .
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.
178 Лекция 20
На эпюре проставляются значения Nz . Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.
Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
где Nz— продольная cила в сечении; А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.46).
Тема 2.2. Растяжение и сжатие 179
Размерность (единица измерения) напряжений — Н/м2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа):При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
Рассмотрим брус, нагруженный внешними силами вдоль оси (рис. 20.5).
Обнаруживаем три участка нагружения и определяем величины продольных сил.
Участок 1: N 1 = 0. Внутренние продольные силы равны нулю.
Участок 2: N 2= 2F . Продольная сила на участке положительна.
Участок 3: N3= 2F-3F = — F . Продольная сила на участке отрицательна.
Брус — ступенчатый. С учетом изменений величин площади поперечного сечения участков напряжений больше.
Строим эпюры продольных сил и нормальных напряжений. Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.
180 Лекция 20
Примеры решения задач
Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.
Решение
1. Определяем участки нагружения, их два.
2. Определяем продольную силу в сечениях 1 и 2.
3. Строим эпюру.
4. Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.
1. Определяем продольные силы.
Тема 2.2. Растяжение и сжатие 181
Сечение 1. – N1 + F1= 0; N1 = F1= 100 кН.
Сечение 2. -80 — N 2 + 100 = 0; N 2= 100 — 80 = 20 кН.
В обоих сечениях продольные силы положительны.
Nz
2. Определяем нормальные напряжения σ = — .
A
Сопоставляя участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений. Нормальные напряжения в сечениях по участкам:
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Контрольные вопросы и задания
1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
2. Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений.)
3. Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?
4. Как распределены напряжения по сечению при растяжении и
сжатии?
5. Запишите формулу для расчета нормальных напряжений при
растяжении и сжатии.
6. Как назначаются знаки продольной силы и нормального напряжения?
7. Что показывает эпюра продольной силы?
8. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
9. В каких единицах измеряется напряжение?
182 Лекция 21
ЛЕКЦИЯ 21
Источник
Правила построения эпюр в сопромате.
Сопротивление материалов
Построение эпюр в сопромате
Прикладное значение науки сопротивление материалов заключается в возможности определения основных критериев работоспособности деталей машин и различных конструкций – прочности, деформации и устойчивости. 
Применяя метод сечений в сочетании с приемами статики и других разделов прикладной механики, можно определить напряжения, возникающие в том или ином сечении бруса (детали, элемента конструкции), и, исходя из анализа полученного результата, сделать выводы о работоспособности этого бруса при приложении к нему расчетных нагрузок.
Именно напряжение является основным фактором, влияющим на прочностные характеристики элемента конструкции, а также его способность противостоять деформации. По этой причине в сопромате главной задачей, чаще всего, является определение напряжений, возникающих в том или ином сечении детали или элемента конструкции.
Для удобства анализа напряженности отдельных участков и сечений конструкции (бруса) используют графическое изображение нагрузок и напряжений в каждом сечении. Это позволяет визуально анализировать распределение нагрузок и напряжений по всей длине бруса, определять при этом наиболее нагруженные (критические) участки и сечения. Такие графические изображения нагрузок, напряжений, а также деформаций элементов конструкций называют эпюрами.
При анализе степени напряженности и деформирования элемента конструкции (детали, бруса) наиболее часто производят построение следующих типов эпюр:
- эпюры внутренних сил (продольных или поперечных), действующих в сечениях бруса;
- эпюры вращающих (крутящих) моментов;
- эпюры изгибающих моментов;
- эпюры напряжений (нормальных или касательных);
- эпюры перемещений (удлинений, укорочений, прогибов и т. п.).
Иногда на одной эпюре показываются несколько внутренних силовых факторов (эпюра продольных и поперечных сил, эпюра изгибающего и вращающего моментов), но такие эпюры при сложных нагрузках и переменных сечениях бруса сложны для чтения.
Как упоминалось выше, наиболее важную информацию о прочностных характеристиках элемента конструкции (бруса), т. е. способности противостоять разрушению, можно получить, используя эпюры напряжений, а информацию о степени деформации под действием расчетной нагрузки – по эпюрам перемещений.
Эпюры внутренних усилий и моментов в большинстве случаев не дают полной информации о степени напряженности и деформирования отдельных сечений и участков бруса, а являются промежуточным звеном при построении эпюр напряжений и перемещений, особенно если брус имеет ступенчатую форму или переменное поперечное сечение по длине.

***
Правила построения эпюр
При построении эпюр придерживаются определенных стандартных правил, позволяющих одинаково читать, истолковывать и анализировать эпюру всем участникам процесса конструирования изделия.
Построение эпюры начинают с изображения нулевой линии, которая символизирует линию бруса в ненапряженном состоянии. При этом, если брус имеет сложную пространственную форму, нулевая линия эпюры повторяет контуры центральной (осевой) линии бруса, и имеет такую же пространственную форму.
Нулевую линию эпюры обозначают названием и нулевым символом. Слева от нулевой линии указывается название эпюры (эпюра сил, моментов, напряжений и т. п.), справа от нулевой линии ставится цифра «0». При указании называния эпюры обычно используют символ изображаемой нагрузки, например, внутренние продольные силы чаще всего обозначаются буквой «N», поперечные – буквой «Q», эпюры изгибающих моментов – буквами «Mиз», эпюры вращающих моментов – буквами «Т» или «Mкр», эпюры напряжений – буквами «σ» или «τ» и т. п. Рядом с буквенным названием эпюры (или под ним) указывается единица измерения (ньютон, мегапаскаль, мм и т. п.).
Следующий этап построения эпюры – определение границ силовых участков бруса, т. е. таких участков, где внутренний силовой фактор в сечениях или деформация бруса изменяются по одной закономерности (или остаются постоянными). Как правило, границами силовых участков являются сечения, где приложена внешняя нагрузка или (и) площадь поперечного сечения бруса изменяется. В некоторых случаях, при построении эпюр брусьев сложной объемной формы, границы участков определяют аналитически. Границы силовых участков обозначаются тонкими вертикальными линиями, проведенными от изображения бруса через все эпюры.
Для оптимальной наглядности графика эпюры важно правильно выбрать масштаб изображаемого силового фактора, напряжения или деформации. Если масштаб окажется слишком мелким – эпюра будет трудна для чтения и анализа, если слишком крупным – она займет много места на чертеже.
Если учесть, что для одного бруса выполняют, как правило, несколько эпюр, расположенных одна под другой, то крупный масштаб не позволит выполнить построение эпюр на одном листе.
Для правильного выбора масштаба эпюры предварительно следует просчитать значение отображаемого фактора по всем контрольным сечениям бруса, и после этого определиться с масштабом.
Если, например, в результате расчетов окажется, что вся эпюра займет положительную область (над нулевой линией), то при построении графика эпюры это следует учесть.
Положительные значения фактора откладываются вверх от нулевой линии, отрицательные – вниз. Если на каком-либо участке силовой фактор равен нулю, эпюра совпадает с нулевой линией по всей длине этого участка. После построение внешнего контура эпюры на контрольных сечениях проставляются значения фактора (обычно на внешних углах эпюры), при этом знак фактора (плюс или минус) не указываются.
На положительной области (в самой широкой части) ставится знак «+» в кружке, а на отрицательной области – знак «—» в кружке (см. примеры построения эпюр). Иногда знаки «+» и «—» на эпюре указываются сверху и снизу цифры «0» (справа нулевой линии), тогда на площади графика эпюры эти знаки (в кружках) не ставятся.
По окончании построения эпюры по ее площади проводят тонкие вертикальные линии через равные промежутки. Эти линии символизируют сечения бруса. Иногда, в случае построения сложной пространственной эпюры, линии выполняют не вертикально, а в соответствии с проекционным направлением участка на графике эпюры.

***
Определение знака фактора на эпюре
При построении эпюр внутренних силовых факторов или деформаций необходимо правильно определять знак фактора на данном силовом участке бруса. Для этого следует пользоваться следующими общепринятыми правилами:
- сжимающая продольная нагрузка считается отрицательной, растягивающая – положительной;
- поперечная сила Q, направленная вниз считается отрицательной, вверх – положительной;
- вращающий (крутящий) момент считается положительным, если он вращает «отсеченную» часть бруса против часовой стрелки, отрицательным – по часовой;
- эпюра изгибающих моментов строится в соответствии с «правилом дождя». Это правило используется следующим образом: если в результате деформации от изгибающего момента исследуемое сечение прогнулось вниз, значит, эпюра имеет положительное значение (образовалась «воронка», в которой может задерживаться «дождевая вода»); если же балка прогнулась вверх, то эпюра имеет отрицательное значение («вода» будет скатываться с балки). Более подробно о знаках эпюр поперечных сил и изгибающих моментов здесь.
***
Особенности построения эпюр поперечных сил и изгибающих моментов
Для облегчения построения эпюр и контроля правильности графика следует запомнить ряд правил, вытекающих из теоремы Журавского:
На участке, где равномерно распределенная нагрузка q отсутствует, эпюра поперечных сил Q представляет собой прямую линию, параллельную нулевой линии (оси бруса), а эпюра изгибающих моментов Mиз – наклонную прямую.
В сечении, где приложена сосредоточенная сила, на эпюре Q должен быть ступенчатый скачок на величину этой силы, а на эпюре Mиз – излом (изменение направления графика).
На участке действия равномерно распределенной нагрузки q эпюра Q представляет собой наклонную прямую, а эпюра Mиз – параболу, обращенную выпуклостью навстречу стрелкам, изображающим направление распределенной нагрузки.
Если эпюра Q на наклонном участке в каком-либо сечении пересекает нулевую линию эпюры, то в этом сечении на эпюре изгибающих моментов Mиз будет иметь экстремальное значение (минимальное или максимальное).
Если на границе действия распределенной нагрузки нет сосредоточенных сил, то наклонный участок эпюры Q соединяется с горизонтальным без «ступеньки», а параболический участок эпюры Mиз соединяется с наклонным участком плавно, без излома.
В сечениях, где к брусу приложены сосредоченные пары сил, на эпюре Mиз будут иметь место ступенчатые скачки на величину действующих внешних моментов, а эпюра Q изменения не претерпевает (приложенные к брусу изгибающие моменты не влияют на эпюру поперечных сил).
***
Примеры построения эпюр

***
Материалы раздела «Сопротивление материалов»:
- Основные понятия и определения
- Растяжение и сжатие
- Смятие. Контактные напряжения
- Деформация сдвига (среза)
- Деформация кручения
- Деформация изгиба
Правильные ответы на вопросы Теста № 7
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 3 | 2 | 3 | 2 | 2 | 3 | 1 | 2 | 1 | 2 |
Источник