Как построить эпюру перемещений ступенчатого бруса

Построение эпюр продольных сил — формулы, условия и примеры решения задач

Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.

Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.

Но всему свое время. Сначала немного о терминах.

Основные понятия

Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

209

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.

Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.

Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.

В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).

Что такое эпюра продольных сил

Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.

Как построить эпюру продольных сил

Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая. 

Сопротивление рассчитывается по формуле:

где:

  • Fl – действующие на участке l силы (Н);

  • ql – распределенные нагрузки (Н/м).

Порядок построения:

1. Рисуется схема балки и механизмов закрепления;

2. Производится разделение на участки;

3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:

201

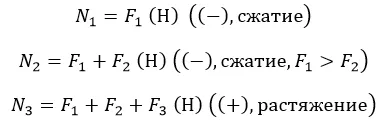
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;

4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.

202

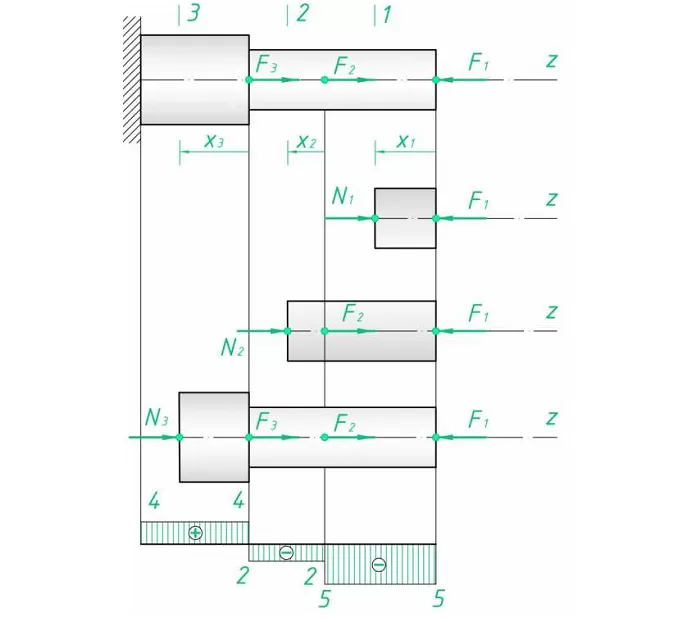
Рис. 1. Эпюра продольных сил

Рассмотрим случай:

F1 = 5 (кН);

F2 = 3 (кН);

F3 = 6 (кН).

Вычислим:

203

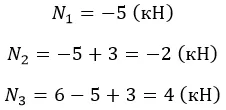
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.

Пример построения эпюр и решения задач

Построить эпюру сил для следующего случая (рис. 2):

204

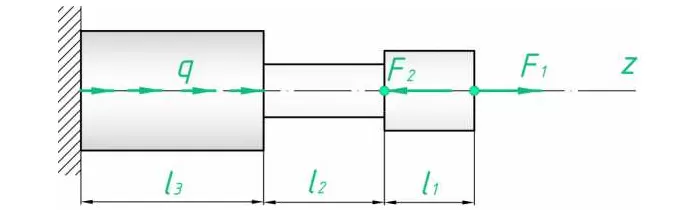
Рис. 2

Дано:

Решение.

Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:

Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.

Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.

Читайте также:  Как построить дом из бруса самому правильно

207

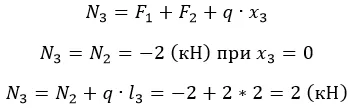
По полученным данным строим эпюру (рис. 3).

208

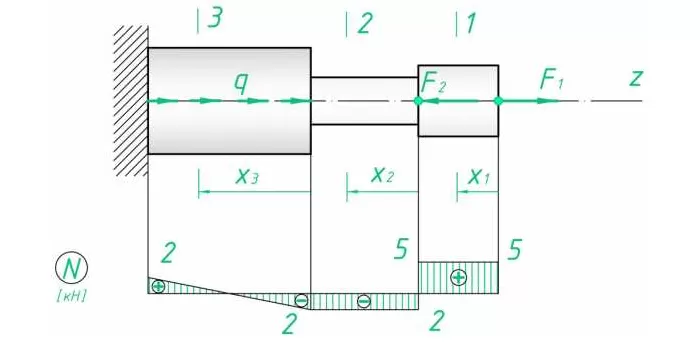
Рис. 3

Заключение

Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.

В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.

Источник

‹›³qÐGGõÏüÀ`Š¦Æäáú±õ´Uû7½jTÎØEù/ûZŠñÛÔV
K̐Ž“k.ŠQ™^|é|ùóèèpÙ=ïE‹n3-›ëÛ좞ŽŠa¬ºJQjyÖÃêº3¾–ŒgݦýÍ|;dJƒ˜V“¦žfÿ,
.ÎM+Ù=¯iÞ§ƒrZoޜ
03Us÷6ûZÞT³fz÷¦3¨¿•o³îÉdXŽhâÐ}¡W`ÍK÷Ç·†â‡/YÐX–F”]åÆñÜIɌÓÌb‡ÀÂzɬXW$ †ö¾q!ڑ…÷!Õ{͌7,~ÃÛÜ ãhÇ=s’» rkââLÞ*.÷nÞ;µJÝ5ÖÕpÀZð¤£ÎÁPi”飋’io™Y¥¨¶|!ɍºÕ~©M1çxßJ—’rK}!|-14À[[Þï︺iƒ
ìKØÍr:„`هñu=À2/VìàÓbQhxÖ«ÿW0*qz‰åùúl€ìIT)ýJ°2°:êü¿°ÚÞÿb~¯ªqgåÓj:kŽo‹)Sr!ïsњ€
îWeú£ì͗§…I5hniQéx]~¶½À…Pv`Å/&+žG:‘,pm³>ü›Ñ€°MA.drѺJDCÛD ¦%$§4ó¦%$PJð$éD÷¸úa-îƒG~¤®s£Cc#J¨Í‰‡,Ñ
Ø+ê*7¤±qCÒ$?
:Šßò¾
(öZGjIÌIþ’n‹’9´-¶PË#¹Á/VîÃ/òuùå`ò[Àtþ[€éÁ(ö£«÷¥š9±l’
ð³B7|g²YýFKsAÎõ{bX¶âñZ·F’^۟{‚ñtO‹÷Ӈ©ë7§ž°#õ8¾Z¸àHŠpQ;ÃÅðM¸œlnԄ‚gßʄi!ãÄ;§÷¹›=̯&¡]3¥stŸÈÛR¶Rç $H—ë`Ú,6¶^æ´}SI$&‰aKÏä j
g½FªÂoËòÄO2ñ”àmjé YcR
%Ò.Ӕ}AZ³g[­M¦Ù+“±/ešà_ :bt.~’è̞”³žÝþÂìÆ:³á¬ä-y‘gªI÷*± š9•Þö·á+i‹+Þ
éP‰ècBæQÌñ±~ÌÅ)Ö¢]Í~â­ï2õ=›† ¹ÿ ɐ»
endstream
endobj
231 0 obj
>stream
hÞTÁn„ †ï>Å»ée5¦‰á°Û‹‡m›j{ga4$âÁ·/ uÓLæf~þ!×öµÕÊùpFtèaPZ:œÍâÂG¥¡  •ð{–n1q$4wëìqjõ` i2òŠ³w+Ò-Öþà„ÚCŒÄ!#×·o|B ©ñûջД»¶‘8[.Ðq=»49=sCý µü_ÏÊ­ë>léãy9ÄP9‹°*¬Î ÒzƒÕ6x‡—ëêP°0ˆþúq7‡±8¬¦&CъÒxìØOö+À ñyÀ
endstream
endobj
232 0 obj
>stream
hÞT‘Mo„ †ïþŠ9¶éE­mbHÚ݋‡~¤Ú½³8Z’Šõà¿/ê¦ òiFQãT­ÁiŒ@¸b/$Z)æíæw1p
Ä&×ë4ãP©n„²ŒÈ—
N³Yá®i҇øȇiÑHÕ[’Ñï‹%õ¢õ/¨fˆ1h±‹Èéëw> ŸxƒÍª¨¿’ÛÛc‹“æ
W=BӔ3wÏPµÿã{Öµ?ÜDV–çNÑWYõÆwUHºÍ¨W’1s0Ë%’— ‹ » ÏææOá±
n¦¦¡f‘Ý[˜ím…Fܜׇ?b1ÆZçâ
rÖH…ÇÌô¨nE öUq
endstream
endobj
233 0 obj
>stream
H‰¬WMÛF½ûWè¸jf¾©Šz­n›v;@€^šCþI~oɎ43’](ÚµW£GòññCûC_¾~žN§Éz˜î’­@™AÑOþ4zPã€1€•¦¿NjøB×4ó¯ï§—áÃôõdhãq8ƒRa˜~9Ñ_Ëg^œæû„ï_Àɜs€FW ùƒ

tüπv?¯ž/^‹çn㹏Øaú3Á¼PCƼ߂{°ñhöð˜r’AŒU
fÁ7T»,‰ý³füpÖ ‘Oåç¬þI
ÛèP€/™;OrÁSè¡|&WÑBþø¹Œ¡¥!@ÉåszKClñ›Øc»˜mbì©6‡ÓèÄb¶…l« Û*ºgè¬0¬,Ö8!
mvÖß7êv‡ÔÜkZˆ
Ï×,Ô{þÞ£?PEÎ˜¦}Jö©z㔈$ø»ë}ÂÃSp°£Nƒ:Žô*jÉ¿ÔÞÙR[Þ7Œé|B¥{ÁoâJMï.Éäz¡$ۖ¶ëöÂÔ%̸§è$‹q•JŽ¹E6Ðv֟ô¯ÍÞ
¨4ÄÀÓɇ|Œqþ¾î2Ìt?lŒ
 é)’Œ±äҒD¬*.@Üí¹û±-òwÏIn—¹°?‹VøíÐ[tˀª£Þ=îk-8Æû|=kÅýF‹¦süsú½A›Òë‘[>„ÎyrwîólÆC],4uleXŸßYi?:ôrpÕLÚ}ÄnuÉ¡º‰.ñÙýa7>Ót‚‰zŠ]&±ËX=˜W0cªrë݂¨¯ÎR]
/}R]šÇ‘âÊ;b#D•‹«.÷¤.S ·þXPþ)MÎm§A‰ÅÛG’,O±;º)õAå»N;ökLØ]“z[ëöZz.Â̂¼ÒârëÅ».úiUê îOá]»çïëäM#Dø–w¡7Þ*Í7}nÓãJmÓ¢œá?½t«6Z$›vd^_o}5i³ø“¿|úлŒØ÷¡W靉l»vŒ”œœ˜ñ»Ö¼áßÛ§ñ¥dwÊtøH˜k)¯KuQcÐ]Ѡ̐.yäÚNï¤*.õˆMY|ÚôBÅY;זµ|I¹{XÞ¦ž‘ËeúöéžÏÅ+‰æ}+báz†pIÛB+rT7«X›~Ë¥“–ÞyûT[ŠŽ€m
:š–µR’ü–šK±ÚÿËj…¶.¢‡^¥úöhŽò»z}“œÇM®žËÇWÕãêėž~¯
¾ïë±w¼ämøG€ W›n
endstream
endobj
234 0 obj
>stream
H‰¤W¹ŽÛ0íý,½AÌð> ÃE4©ÕeSØZ»°Mþ¿ÈðEÒ´¼[ôj¥7×{3#‚¦y·G/ÓßÝ·i∢é¶ÃLJDÐôcwÀ„ãž9&gƒó
×ù^á†)¯
ˆ»»*íàzƒßp*wøûþç¬i-± %± d°öºöh´’maŽ%s.³†£˜pÙóœÖžMH>ÎI^£ [‚Ö`®±Pè@15É;êüí¼»À5Ç4¿”ÂMmàâ!JþL¿
kK1ôë»ëÉwøl‰ëÚ÷¥„éáýëK¨iaÏ9ÍÖ X¦lŽ …‹¤ÒN½ 4È䊠»=΅]s`—u‘¸ÚçÐhÅUE£ÃÝÓ@ç=MÃ×®1>4f[½ÁKCm@$¸Ï5«g%;î‰-‘b•üŠ)ʊ‘ÎHü=GZ‰+3®ÏbOڒ“aû¬:Wå÷15Š—zÜ>>¨@ˆkD³êWGUiP©{,½!VG9®îÊǒ¯ÞÇsðÓQHÍ5°ÖC]—Þ¦àÓèñJ»ÆF+Zî€T‰ýµïMLdŠìžcï¸5à†Pëyfäå^:ø¶t4

Z·Í¸õ¬,ؒn6Œ¶•®Q³bÃ;0ƒ…^tÌC/7¦/MÈáèð×ává¨N1=$´7_UÃƳ¦ÖšsËI1žÿ%x¦MÑ(ëAK±arÌrÒ#Ç»ØÅ*“нÙHù3öxڕüŽ¤ãžD0÷q(ÖÇeâd£¹õêd¤®XûŠ
ìYl}NŽKÇX™4uleFŽÙfç¹ejåžJ¥U‰„EæžÂŒÜ|ÚÔr—¤Õ”Õ­ØI6†ýéÝMm
ë¡«†’õ0꯱Í5íÌG9ÿH¡ø`“´KR=¡eµ‹5jQ¶Û³Xz9yÎ_õÔ¤¢^µ÷õ’Ýæ’Ìy÷ööG‚a3^۔‡OÖÙÌI:¾¼³3åގӝå†ô‹æ§´^î¯Ð£]%ЮE¿b‡°3†¤Ö˜Ùû“[êiÛÏIûç´ãDb­À3øxbˆq¨¸Bð%b­Aÿ®»ÛîûԍÈHè;H*_xŽNïëUïºôžþ–iú¡ÿ ~žX
endstream
endobj
235 0 obj
>stream
H‰ÔW»ŽãFÌù÷€S{==ÃóBÁá.qÌÌp°«].ñÇø{Ý=/Ό(-m؁‚DV?¦ºº¨æõ2=͟ÖߧŸÖUÏz^¯7«yý6RŠäŽ_Ÿ•q¯ÊÐÞא¡×ó Hþz9ÿ¶þ2}_§à@…Ù‘Ä™31
μO×éë*aL
£
GQ3_4z°ü”K|ëúcR1/(‰azâĀv>iÐAÒ{2À_ëM6Ýd ÉÞ gˆ!à-§møûõÜ![ИS]KìВ“ †ŒJKj‰“Ï%!“‹ýЃ:ŽîZô mæÏ%7_ê¸òÕ§h~é#90‡ã`Žã}Šå%֐¹kºÌ!#š1…:i‹wñˆ|üy;žL.þÇîUëº,šš’I»=,¤µ¡…µ¥‰Cóâ]Òïµy¦“w„¨ÌÒºäýžÎ|ã ð±TÁ»Lâ‰I¸rÚorux;vÂp©÷@°Ø£8Ær󐛇ïãùèŽzŸG0Ê¡$•ËJT~RôÜÌl}
ëS÷‚ýŸNêïvø;ã¡SҌ¨4bÒòP™:*Ue
iˆ¤òˆ*]¥QóTÇ­S|²6-üš4KgH²=¤¾C×û*÷ÖÛ&Òô~֔v—4ãÚjOËÚ^풪ñJ¡níÜhšÂ&t©C–N]ס]Eêîh} äKς·•–¡¤—}”~¼Ž–mTÓëŒY´3á/#®ÖÝ:hçxùG–¢e*êÛ£i»”A‹4(Ñá¼2½‹Yؚ@Ñ”M$œ6¥ØØ=—Š
dñj.vyÎþázSðþ¾³c”ÿˆÁý;$`WˆÙâ?¦§?ÇÜ|S¹.•Gsi$¸ªòD¼¿¦“E?°[,ïËìŽë>ú›j™qQb–µr¢ò]ov³ÜÞwéfá6±oö­¿7»67ɧlÏ¢>_o–]׍/½{gJõ^QAX£«Ïy›Î¬¨ÅlnjÔvN#Ó]ñ[£%@õލ|·mèȑWÖø^áÁïz‹ÇÆÿu«n¬†
y§=?çӆDÑp§ôâeĬA ¾5€3™›{¿{«yK‹ Hb¶¾ÙÎVÛÎBÌÛ2ýSàü(ß»ý«ž¿Hn:X²”×´²$ ÇÒ¸÷U—»Ý4²¼Ž¬`ñ=þšVýûK#ÀwEKÇHU;ÒÑì¿áìF.ÊZOö­‘0uÁÜÈo¡F‚’‘â­#Ðw ŠÁ€ç[0tµJ´â?Ã^úņeéº7«¶ÚËù/ ùùŠ
endstream
endobj
236 0 obj
>stream
hÞT‘Ëj…0†÷>Å,[ºˆ—X9 KÁE/Ôӳω£jQ¾}“ŒXº0òý™É?VÕϵ`vR
.Ð
ºµ8O«U7ì
I
í –Â©Fi€¹äf›kÝMP–ût—ób7¸»ò‡øØ»mѺw
O¿®NiVc~pD½@B@‹]ĪWiÞäˆÀBâŸxÙB8Ù½§g#Z©{„2N“GáÅI êöÿ}”SÖ­SßÒFGtv΄§LzâIL¤ˆR»$â8’z‘sÙß;^’3–„bxJÑåR…¼ ±»ñDâîùÄR/Y3*«ÈÈÏ{äé[öë8F¨VkÝtÃÎÂýôÇZÍdü üý
0 („”M
endstream
endobj
237 0 obj
>stream
H‰¼W¹ŽÛ@íý*wˆ™ƒœ0I“Z]Â«µ‹ iòÿE8—4ËZ›M!H–t’ºáëá(”Q§ô ó’²”>Þ[ԃ‚‚Ù°ùr|Y¡¬Š®|üLáyiu¶-¶¼
öe±ÿ’lZ™îÇ(þíƒíoÃAj;DÞuÒH¦“á՟Ëázø2 • ¤b ÑñMyÉhH…î†ßÙ#(.ɼB€È‹â“ò³XÇ>ê1ǙaÀ´
‡²„(Ù³%; ?B˜ö¤‘3 ¾&vÌ÷s»ÕO?‡ï9áÖh½ÅŒ©óµ&X|ÍôáhÐhõ>€AË/–o²Ñ/’ŽÙ›’ô—ÄCÝxǒ°›Þ ª@ÔÄ9½VO=:&¼I¢áX’%÷ƒi¤H*nK%³-Q¬C| ¤ÐE¹F‚D i+ÐΫ
Ã=2†k³— Xe!éóÍ*H…üÅ2v‰§OmDÆWî€ã5¿13¡âó˜8jùÀ»)Õ«`^O
áÂ8õ’“wL:•»

Источник

ïéñ§w§—{ï̦ƒ–ñZ½ÓxÓ3‰Ô_í¯Ölç¯T¢=³ŒsäÞ¿Œ¾Ù¥-ˆ-.%šÜ“hx8ë‰fÏØÀY$ǏÉså¸ÓK%fZK6´‘lVlúS“M‹?ÉfµÅŸŽ÷?ì¯Sì2œ®¤´…¬
-kå×v†Á¼jgØ{ØD†yù~Å-/eˆó’9s‚ÆY`ëýJÔëKÚaÌÝ֖¶yxÓ²Ò¼–sW^dêQݖuŽÏÏ[7bÛº
¼`ÝU‚¡]¥^ô¶Á#Mx»æ}¯¶ÏhÖ¹>­7½ZÝ«MZyÙÖ7h›:Äh¯,éÞ¾©Ó±”ӝÖmè˜3®Wk[¼ìÃѧ÷ïw_±#ݤ¶w 6g©Ùdï»Ý¶×ûÍd7˳ðàírœ»ëÿÍA~ŽÿÚ£FdRâw€óLŸ?j잛v;d¼ä±CÌ-ö^ËÆncðæA۳ȧ#ýóv˺ü è勉-É-™T/¦q؞ä¼Í±ñÕo(àHìv%Þ~w’_Ь˽ù»w¦9&4¯ŸQç^µ ½j«ûÕ}„é}c×?2ßGX¾‡Î`ù ¶µoyÁ»Õ^Þeö,¹~µíUS¿UR¿U(õ«;’†uû‚ç!:KAº8pÏÝ|ÈV„Þ¶ŒÐ!Ýiìà í¶µáO;:ÛzEZ÷Œ*å>[¥î¢çK:mÅo€s§­à9©;Àâ{µ¶ÊŒÛi+â™K¦Üi+~ßM¶»þL§ÓVØW¦n‡æWˆÝþ̟Q÷CuÚ*ñ‡B¶»î¹ÓV™{î´ñ˜uŸ%çñý· ðX…
endstream
endobj
4663 0 obj
>stream
hÞ4ÎË
ƒ0Ð_ÉÄL»”,úPU…Ò…•P(µ)6?¿3š,Ͻ$w@KÁ
¶ÛñCx‡Ù}‡Ñ~†)¨ºXËOKl»UL©ªÃ’bÚ÷kª)%H|2 ¨*$B Š š&UºoÒH7‡Ñùxãݱæ½_»o§áé÷w~=?^~¤ÚIULTÛÏ턢€¡2Bgh„É0ˆr»ÆÚ¿ 9Jp
endstream
endobj
4664 0 obj
>stream
hÞ225³T0P°±Ñw­(q.I,I²Ýƒ
LÌLŒ€2Avvúnùy%@ѐ°¨)HÄ1T0234ƒñ́H¡9”c
”10rÌ@3¨ÁEùÉÁ©%Ñú.nú!©%±vv 9#‘
endstream
endobj
4665 0 obj
>stream
hÞ,Á D…? @›4ªm8Ùã ib¬˜Ê¡Ÿï.e/›7³3Ëå±%
é:Ú§wZíׇˆð-áJ¢wR
CКž·Ž–¡¯Ö>TçŠ*K€Aœ©J­C‰Å¢Bù¢jÕ´¦`c¾Óé4P·LÍâçØïË´î¥æ/À £{6û
endstream
endobj
4666 0 obj
>stream
hÞ,Ë
Â0E%iR¡dSmÉÊb²ÄE¡ ÖHE?ßLÍj8÷pïˆæÐFºŽöù•W÷ 1!|E„Rº¸’FR•P1Ž`=m0:€µÑq»•U
ù
%õ^`ªk:­9º7:êÓÔ.aNýÿØ;½žÏ±i.‘íþk§²ßÖyc~ H)1Ô
endstream
endobj
4667 0 obj
>stream
hÞ4ËK
€ …á­¸©„“N%Eƒg‘QwÐòó†
¿ÿp„jÂHÛÒ.íéòçºEÄ­‰ÐŒçi2†X+àd=’RKQ¦1k_UX3¢.¨2+ˆÿì®´ù3uýHC|`1æ` Áª%Ž
endstream
endobj
4668 0 obj
>stream
hÞ,̱
€ ÆñWñ
´KÍ@œJ×H·hˆp-ˆzüθí~ÿ´sB ïåübÊx`¥;åNh«–5節òWÓ*FO0Š¡€1°jd8B§øíòÜg®¸ÉeŠ²Ô÷> Æ=#2
endstream
endobj
4669 0 obj
>stream
hÞ22±°T0P°±Ñw­(q.I,I²Ýƒ
LÌLŒ€2Avvúnùy%@ѐ°¨)HÈ1qÌ¡c ÇÔ Ê1q`šŠò“ƒSK¢õÜôCR+Jbíì ºŒ¸
endstream
endobj
4670 0 obj
>stream
hÞ4ÎA Ыpƒ
“†MµMW6ÂÂĸ@BLŒSYôø2͸|ÿáKµçŒ³¶….¿òâ>!&Ä×0i¸¨ÕÙZ8®ep%¬’˜2JRÕçw©©÷[ª1Eðú4 ”!Iš
Í
! (¶ÆЗӒ£Kå
Ó¡ŸÖã©»Áåt¦ˆ{ÆY0A­ý 0 •{9M
endstream
endobj
4671 0 obj
>stream
hÞ,Á
Â0D%°MH»BÉ¥ÚғÅä ˆ‡‚P¬‘º‡~¾Ù²Ç7™Qú(E#Úºò.«ÿƔ ~V(ېº:ç
I
^
mµb՗Ö4„=5”ÈZ—–I‘:0è
F1zÑû¥åÝi-Ég¼Ãtê!ä
aâ+w¸]žsNt:.JH.8÷` [>stream
hÞ4Í=
€0ЫômCZ¤“ÖUl7qéª `ʨ¾×ãCS¢J­§dzä΂Ž×I5ÍùK§«À[/n5¬p puÌ À3þ–y2ßב
­z¢Îå¡-„W€ ó&
endstream
endobj
4673 0 obj
>stream
hÞ4ŽË
Â0E%wT(YøhéÊb²ÄEAk¤fÑÏ7SÇ幇;w„ÚHÂHÓÐ]~æɽCL C„a¼ª“µô0—ΕP@uŽe”@ÕæW©©÷Kª!àµÎ
’ µB4CP AäBXöÿÖpáâ0åèR¹ÐaßRŸæBû1ÜÓöJÏÇÛ#Ex§%òW°ö+À im9′
endstream
endobj
4674 0 obj
>stream
hÞ,ŒA
ƒ0E¯’Œ†1RllWJ“E¡t‘†PÚ;oÆfùÞç?‰’…hhã;®æë|`ø)!UQ¦éª56ê
9â©7¥@…2O]üP²Ö¶b›@2Ô*Na†£«òyZ£7î0;°a#÷
ínãsžËÂBÖÿƒÖ» ·.
endstream
endobj
4675 0 obj
>stream
hÞ4ÏM
Â0à«äùi’Z(ÙT[º²4Y⻆ ˆ5R³èñ͔qùÍ#o2B6Š0Ò¶´K¯´ÚðÕDhÆK4CO[lö¢Ár»µõéËÔ¹}
]3€—ç£D5¢*P!¡`¥Dìûÿ5 A šáúiMÁÆ|¥Ó±§.n™Ž‹ÄîF/çû3øÛ¸(Rá)Æü (ÿ;ì
endstream
endobj
4676 0 obj
>stream
hÞ4ÏK‚0à«ô}PZHH7(¤+‰eab iLŒXƒ]p|;e5ßü™G…¬a¤ih^auŸiö€/gD(®SvNR Œ#jH*€1ô¸ÅÞÅ)BWï8‘J
ŒºðŽ©:Ž¹Zæîí
% ҈»¡d ˆöKD>æ? ‚i7k˜W:::ú-R»LßÑËéþô3eEŠ}±]4)ð?Æü Á°CÀ
endstream
endobj
4677 0 obj
>stream
hÞ,Í=
Ã0à«ø¶UY¡`¯1
9~¤¢Mß{øœp9ûåâ­ò—»Ü[ AšW)~’KÚÚ?Mš*¢Šd­&ÃC‚`H² h ٓý7ŽÚùí÷yõ­_ü)å`  Ó&
endstream
endobj
4678 0 obj
>stream
hÞ4ÍM
„0à«ômcZ¤+¶2ín˜…H·
’…Ç7‘Ì.ß{$ì;ãÌ0Øé¦%ÓF•ç%{ƒ›OJv>ⴔ7
’
¼è£
¤j
#8
@xÇ¡»
þZA¯èä´Ó÷ëuî¹Ò×®ãlK½é—Ò#À ‡•+”
endstream
endobj
4679 0 obj
>stream
hÞ4ÍM
„0à«ômcZ)HWþleÚÝ0‹AºU,˜’qfìtÑRèOç¥xƒ›OÎv>vâ´Ö’
’
¼è£
¤ê#8
@xÇ¡»
Þ½ éÇõ` ƒ¢(Û
endstream
endobj
4680 0 obj
>stream
hÞ4ÍÁ
€ àWñ
œC
A

E£:½3tû~í–mÀú–&)m`Á Áb¤!¬ùŽ°HA‰ÝœÆó•w‡š÷qɼ†Gܕ²/¥½ñËéþŒ#~®àR)J(@ä@Çxÿ` ¦2I
endstream
endobj
4695 0 obj
>stream
hÞ4ÏK‚0à«ô}ÐLH¢VËÂĸ@Ґ±»àøÎвš|3mÿ©PFʒVþíûF‡øA[h‘Ãì
Ò ÆÆÐó†€Ë‰ÔR¤Qí?º}¿uÕvá[Y’ÀQžK‘€ùL&lù:…t‹­wڝjÚ»5Ðv&wŒ¥Š¥}ÐÛåùr#îÓÎðÎb(@Š9à°£ œ³˜cÌ_€ †FÎ
endstream
endobj
4696 0 obj
>stream
hÞ4ÎÁ‚0àWÙllHbv…p’8&ƒÅĈ3¸ï:ÊiùÚ®ý¥ÍÛïyåß~¶ßatˆŸfRˆ­‹1ü´„Ɔ!`«±ÀrKjÕþbµïSUañ{ڜ”EɌ$q° dJr„$(Ršm]( ;o§áéëSÝùõüx¹·”`=ÐNRD¨
¡7Ȉb=`Ì_€ ‘8IÑ
endstream
endobj
4697 0 obj
>stream
hÞL‘_kƒ0Å¿J7†ä&Z(BmgׇuRe+”>d.X‡±uß~71…=þιÇsodœÆˆ Æi‚X²@Ë%^ëNOå(keá*„ÂÌ!MñóÍlK#µ¶%E‘ˆ˜·r=P«Ê©Üª»ˆ³Ä³Vì!àÄCdyà¶2òàú…‡ØÂÂl,(ñõŤëR™.69®ÔÍà]/•ññíó[Õv·]ÏBDلwà Ñ ¿C æš4…Ϭ®µJ¯åø¢Úæb%„àš­€QóN6WFîe²LßNç
BWÀ4D˜8;7—}Ûý>Tm¯®h¯~ÐA÷rxœ½¶S6p¿À){Ù+¼-òuQ$ (ƒLw_¯•+ͤL}Á{=õ²sÒǼk«îŒìÚz54B—FõW¿£r³ö–©žðñߍiú’À Ür›7
endstream
endobj
4698 0 obj
>stream
hÞ4ÎË
ƒ0Ð_ÉÄL*}(®*‹BéÂJ(”Ú›…ŸßM–ç^’; EÉ2¶ÛñƒûÙ~‡Ñ~†ÉV—ªâ§%46ªÆ
¦Œ‚XÕþ0íû5Ք$>T塳E€M“*bÝ7q¤›ýh]¸ñîXóÞ-·Óðtû;¿ž/7ÒírûQ»D¦BB‚@È@¨‰Ð
a4″O0ˆb;­ªþ ²M
endstream
endobj
4699 0 obj
>stream
hÞ4ÍË
Â0Ð_ÉäÑ$U(YøhéÊb²ÄE
Ak¤fÑÏwÆ&Ës/3W(Á#MC÷ñgû}@|5šq¨ÎÆÐã’:›Æ„Ug9‘ZŠµñ uîŸ*LQgT Å2$¢sô6¤+-uaI´ŸÆGØÝèåtŸû©ª _÷@U°ÈÉ ª€ô:cÌO€ ¡‹9Ž
endstream
endobj
4700 0 obj
>stream
hÞ2252T0P°±Ñw­(q.I,I²Ýƒ
LÌLŒ€2Avvúnùy%@ѐ°¨)HÈ1qÌ¡JŠò“ƒSK¢õÜôCR+Jbíì 8·2
endstream
endobj
4701 0 obj
>stream
hÞ2252R0P°±Ñw­(q.I,I²Ýƒ
LÌL@2Avvúnùy%@ѐ°¨)HÈ1qÌ¡JŠò“ƒSK¢õÜôCR+Jbíì 93
endstream
endobj
4702 0 obj
>stream
hÞ,ÎM
ƒ0à«ä1c~(H6¶Š«Jã¢Pº°
¥6Åfáñ;£³
ß¼oÀ@)
QU²Nﴄï8EÂO9˜]PQ(‚÷ò´æ6ä1ÓÇ6(¡­ŽšôÉ8†mj¶m„ÂueY@‘c”S04†*5cë·Ò/i
1ßdlä×,»y|Æzº»¼ž¯8Ñ!݌§)ãöMïÿ ¢¨>stream
hÞ,Œ1
À ¿âÔC/X%ÚJ´)B°®ðùÑpÝÎ,X0B çäÖ)fº¨Ž³
Œ²{/C{hØR~k§  F&˜ia°£(À¯ÒÛîéi
²ÔN§÷Ÿ Dö –
endstream
endobj
4704 0 obj
>stream
hÞ,ÎM
Â0à«äù.J6Ֆ®,&AÔ
bÔ,z|gÚY…o^†7Ê*Ë«*^çw^Âw⒏L9- »‚@H„÷ü¼–6”¡àÇ6HfœQ5ùS`ã6µÛ6@ºt$…с VB,VÂÖ﨤_òR¹óþÔð˜Ö»y˜R½?݃ß.ÏWñn6šIg÷Mïÿ žÛ>stream
hÞ,ÎM
à à«x¢†Bp“6ÁUCuQ(]Ø …ÒԒºÈñ;šYÉ7ÏáPBFºŽöéV÷
s,øñºá]@À*Œ¡§-.‡>ŽŽ©¥ÀhHŸSïëTÕm ‡u®Q¢D-¢(†¡J¥DÔ~%ӚfóNǁú¸ej—ðŒýþØ;½ž¯8—Cì»%á-Û7ù0 ¡V>stream
hÞ,Í1
€0Ыômcé¤vÛMDº*Ho»ÙòþçˆÐg†ÁN/åB5¾sñ&` n֔ì|_Äi­%xèQRõŠŽ»@yエO–ç>K£Í.ãlk{iOé` ,&
endstream
endobj
4707 0 obj
>stream
hÞ225²P0P°±ÑwÎÏÉ/
.HLNqŠÍŒÌRAvvú®%îÁ%‰% )÷`C3#¨”[~^ P4$,j
rŒ@s¨’€¢üäàԒhý 7ýÔŠ}ÏÜÄôTçXýÿ¤¬Ôd~Ï ^Cs¨;;€ x)
endstream
endobj
4708 0 obj
>stream
hÞ4ÏA Ыp`
Ô&
›j›®l¤ãbb¬˜Ê¢Ç—i¦Ë÷g€h¨˜`u͛øŽ‹ûú) ~†2.ÖòӚ:—|ÂQç$SFÚøI9Ç-՘»d>.Í®»
àbI(2´ (4P„­Í~]‰¨èýa‰“éƇcËÇ°&ÞÏþš;¿ž¯0a¹~V†ÉýÆÚ¿ Ó>stream
hÞ,ÎË
Â0Ð_ÉäÑ$vQ²ðÑҕÅd!ˆ‹XBA¬‘šE?ߙ:Ës/Ãe*Ák~ȯ¼øOâk™²BBuqŽŸÖÒùV—L[­¨jó»@–LÎ¥%)¬v„
`A#Áà¤&lû–F†%>•Ž-i-¼Ÿã”öw~=?žiÄú&dýÿ

Читайте также:  Построить дом из бруса в одиночку

Источник

Ступенчатый брус нагружен вдоль оси двумя силами

Примеры решения задач

Ступенчатый брус нагружен вдоль
оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом
бруса, построить эпюры продольных сил и нормальных напряжений.

Как построить эпюру перемещений ступенчатого бруса

Рис. 20.6 Перемещения поперечных сечений брусьев в статически определимых
задачах

Решение

Определяем
участки нагружения, их два.

Определяем продольную силу в сечениях 1 и 2.

Строим
эпюру.

Рассчитываем величины нормальных напряжений и строим
эпюру нормальных
напряжений в собственном произвольном масштабе.

1. Определяем продольные
силы.

Сечение 1.
– N1 + F1 = 0; N1 = F1 = 100 кН.

Сечение 2. — 80 — N2 + 100 = 0; N2 = 100
— 80 = 20 кН.

В обоих сечениях продольные силы положительны.

2.
Определяем нормальные напряжения .

Сопоставляя участки нагружения с границами изменения
площади, видим, что образуется 4 участка напряжений. Нормальные напряжения в сечениях
по участкам:

; ;

; 
.

Откладываем значения напряжений
вверх от оси, т. к. значения иx положительные (растяжение). Масштаб эпюр продольной
силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр
и имеющегося на листе места.


Растяжение и сжатие.

 Продольные
и поперечные деформации.

Закон Гука

Иметь представление о продольных
и поперечных деформация! и их связи.

Знать закон Гука, зависимости и формулы
для расчета напряжений и перемещений.

Уметь проводить расчеты на прочность
и жесткость статически определимых брусьев при растяжении и сжатии.

Деформации
при растяжении и сжатии

Рассмотрим деформацию бруса под действием продольной
силы F (рис. 21.1).

Как построить эпюру перемещений ступенчатого бруса

Рис. 21.1

Начальные размеры бруса: lo – начальная длина, ао — начальная ширина.

Брус
удлиняется на величину Δl; Δl — абсолютное удлинение. При растяжении
поперечные размеры уменьшаются, Δа — абсолютное сужение; Δl > 0;
Δа < 0.

При сжатии выполняется соотношение Δl < 0; Δа
> 0.

В сопротивлении материалов принято рассчи-

тывать
деформации в относительных единицах:

;
ε — относительное удлинение;

;
ε’ – относительное сужение.

Между продольной и поперечной деформациями
существует зависимость

ε’ = με,

где μ — коэффициент
поперечной деформации, или коэффициент Пуассона, -характеристика пластичности
материала.

Закон Гука

В пределах упругих деформаций деформации прямо
пропорциональны нагрузке:

F = kΔl,

где F — действующая нагрузка;
k — коэффициент.

Читайте также:  Построить дом из брусьев в тульской области

В современной форме:

; 
.

Получим зависимость σ=Eε,
где Е — модуль упругости, характеризует жесткость материала.

В пределах
упругости нормальные напряжения пропорциональны относительному удлинению.

Значение
Е для сталей в пределах (2÷2,l) • 105 МПа.

При прочих равных условиях,
чем жестче материал, тем меньше он деформируется:

.

Формулы
для расчета перемещений поперечных

сечений бруса при растяжении и сжатии

Используем
известные формулы.

Закон Гука σ=Eε.

Откуда .

Относительное удлинение .

В результате получим зависимость между нагрузкой,
размерами бруса и возникающей деформацией:

;
;

 
или ,

где Δl — абсолютное удлинение,
мм;

σ — нормальное напряжение, МПа;

/ — начальная длина, мм;

Е
— модуль упругости материала, МПа;

N — продольная сила, Н;

А — площадь
поперечного сечения, мм2;

Произведение АЕ называют жесткостью сечения.

Выводы

Абсолютное
удлинение бруса прямо пропорционально вели
чине продольной силы в сечении,
длине бруса и обратно пропорционально площади поперечного сечения и модулю упругости.

Связь
между продольной и поперечной деформациями завис
от свойств материала, связь
определяется коэффициентом Пуассона, называемом коэффициентом поперечной деформации.

Коэффициент
Пуассона: у стали μ от 0,25 до 0,3; у пробки μ = 0: у резины μ
= 0,5.

3. Поперечные деформации меньше продольных и редко влияют
на
работоспособность детали; при необходимости поперечная деформация рассчитывается
через продольную.

; ; откуда Δа = ε’а0 ,

где
Δа — поперечное сужение, мм; ао — начальный поперечный размер, мм.

4. 
Закон Гука выполняется в зоне упругих деформаций, которая определяется при испытаниях
на растяжение по диаграмме растяжения (рис. 21.2).

Как построить эпюру перемещений ступенчатого бруса

Рис. 21.2

При работе пластические деформации не должны возникать, упругие деформации
малы по сравнению с геометрическими размерами тела. Основные расчеты в сопротивлении
материалов проводятся в зоне упругих деформаций, где действует закон Гука.

На
диаграмме (рис. 21.2) закон Гука действует от точки 0 до точки 1.

5. Определение деформации бруса под нагрузкой и сравнение ее с допускаемой
(не нарушающей работоспособности бруса) называют расчетом на жесткость.

Примеры
решения задач

Дана схема нагружения и размеры бруса до деформации (рис.
21.3). Брус защемлен, определить перемещение свободного конца.

Решепие

1. 
Брус ступенчатый, поэтому следует построить эпюры продольных сил и нормальных
спряжений.

Делим брус на участки нагружения, определяем продольные силы,
строим эпюру продольных сил.

2. Определяем величины нормальных напряжений
по сечениям с учетом изменений площади поперечного сечения.

Строим эпюру
нормальных напряжений.

3. На каждом участке определяем абсолютное удлинение.
Результаты алгебраически суммируем.

Примечание. Балка защемлена, в заделке
возникает неизвестная реакция в опоре, поэтому расчет начинаем со свободного конца
(справа).

1. Два участка нагружения:

участок 1: N1 = + 25 кН; растянут;

участок
2: 25 – 60 + N2 = 0; N2 = — 35 кН; сжат.

2. Три участка по напряжениям:

;
;

; ;

; 

3. Удлинения участка (материал
– сталь Е = 2 · 105 МПа):

; 
;

; 
;

; 
.

4. Суммарное удлинение
бруса (перемещение свободного конца).

Δl = Δl2 + Δl3 ;

Δl
=0,125 + 0,05 – 0,07 = 0,105 мм.

Как построить эпюру перемещений ступенчатого бруса

Рис. 21.3

Источник