Построить эпюру изгибающих моментов и выполнить расчет бруса на прочность
СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр
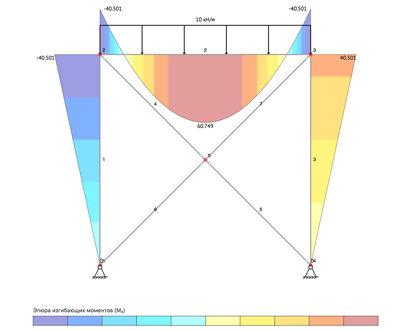
Расчет рамы/фермы
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
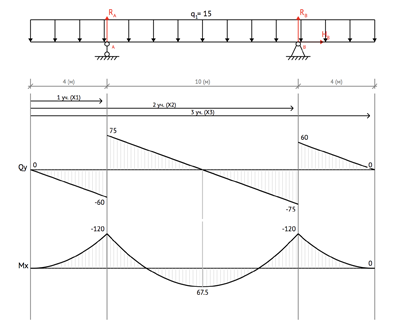
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
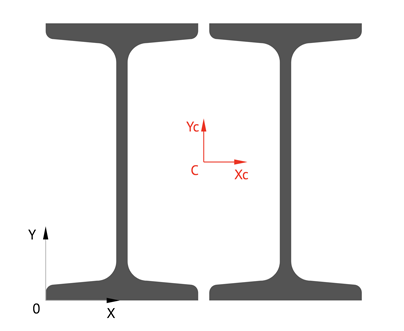
Расчет
геометрических характеристик поперечного сечения
Определение
центра тяжести, моментов инерции, моментов сопротивления
Формирование
подробного отчета
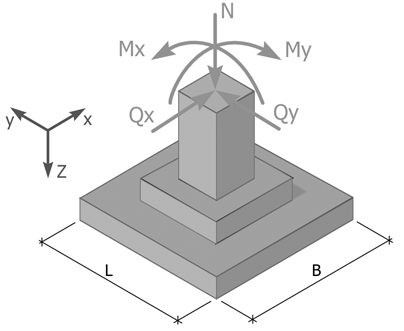
Расчет
столбчатого фундамента
Расчет
ленточного фундамента
Формирование
подробного отчета
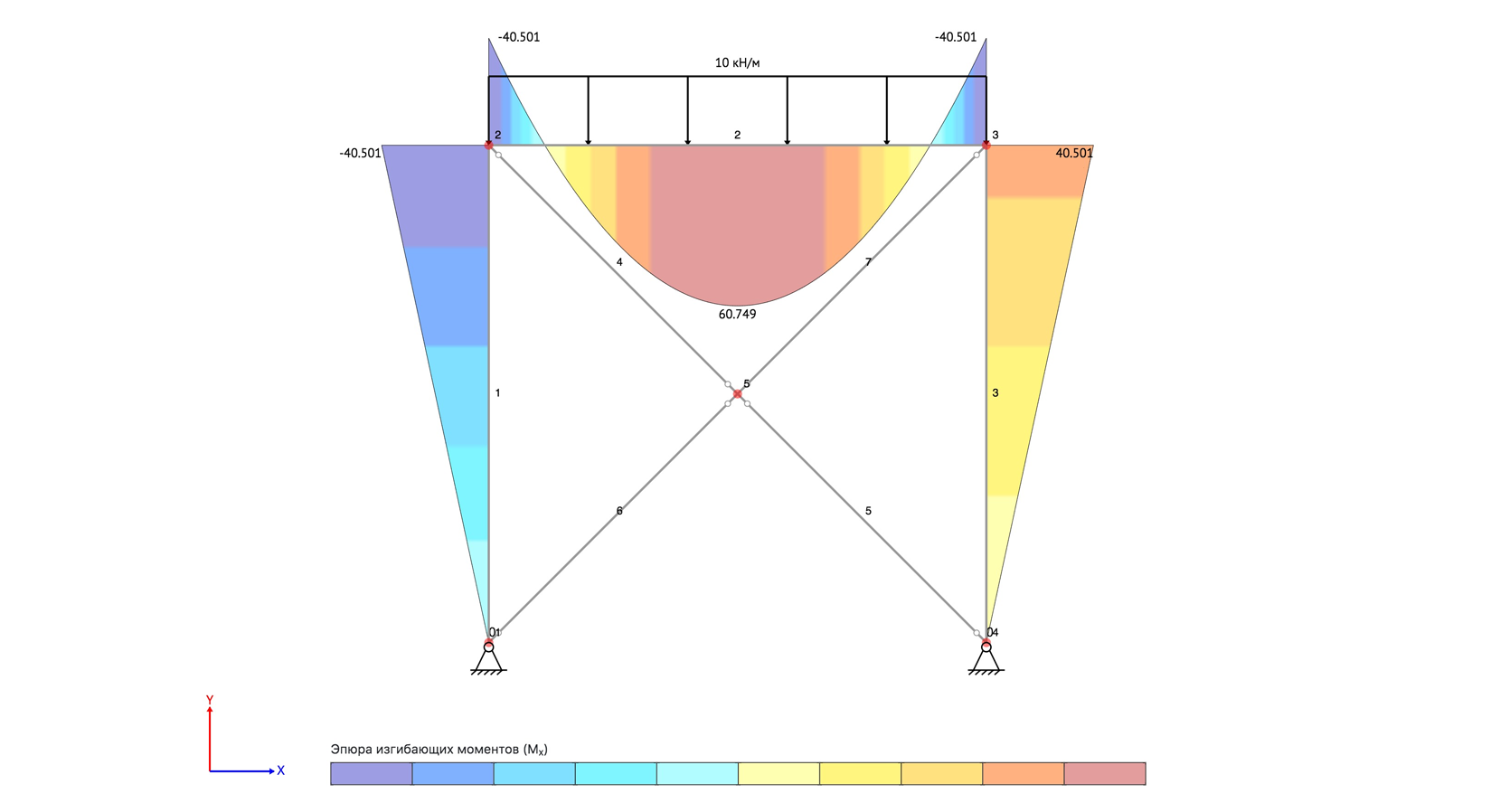
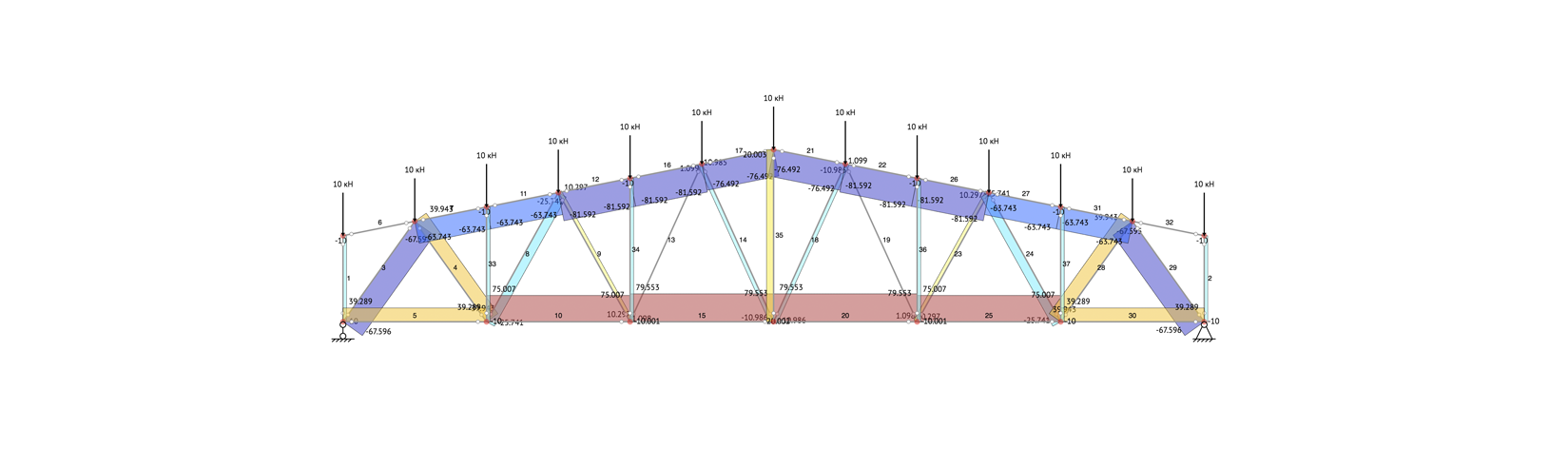
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
Источник
Расчёт балки бесплатно онлайн
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки и позволит | |
| 12 | |
Операции
Длина балки Уточните длину балки, м: Закрепление одностепенное Смещение, м: Конец балки для отсчёта смещения: Угол поворота, град.:
Закрепление двухстепенное Смещение, м: Конец балки для отсчёта смещения: Угол поворота, град.:
Жёсткая заделка Выберите конец балки для жёсткой заделки: Сила Величина силы, кН: для смены направления силы поменяйте её знак Смещение, м: Конец балки для отсчёта смещения: Вариант ориентации Угол поворота, град.:
Вариант изображения Момент Момент, кН·м: для смены направления момента измените знак его величины Смещение, м: Конец балки для отсчёта смещения: Угол поворота, град.:
Распределённая нагрузка Нагрузка, кН/м: для смены направления нагрузки поменяйте её знак Нагрузка по всей длине стержня Конец балки для отсчёта смещений: Cмещения ближнее, м: дальнее, м: Вариант изображения
Настройки Эпюру изгибающего момента (Mx) строить на
сжатом волокне растянутом волокне
/для строителей/Компоновка результата
Объекты
В данном расчёте не задано ни одного объекта. Для создания объектов модели перейдите в раздел «Операции»
Источник
Построение эпюр поперечных сил и изгибающих моментов
Для расчета балки на прочность при изгибе необходимо знать наибольшие значения поперечной силы Qy и изгибающего момента Mz и положение сечений, в которых они действуют. В связи с этим возникает необходимость определения законов изменения Qy и Mz по длине балки. Для этой цели обычно строят эпюры поперечных сил и изгибающих моментов, которые представляют собой графическое изображение функций Qy(x) и Mz(x).
Примем положительное направление оси Оу вниз. При этом на эпюре Qy положительные ординаты будем откладывать вниз, а отрицательные — вверх. Ординаты эпюры Mz будем откладывать со стороны растянутых волокон балки. Согласно этому правилу для балок положительные значения изгибающих моментов откладываются вниз, так как эти моменты вызывают растяжение нижних волокон.
Рассмотрим примеры построения эпюр Qy и Mz.
Пример 7. /. Построим эпюры Qy и Mz для шарнирно опертой балки, показанной на рис. 7.14.
Из уравнений статики найдем опорные реакции:
Установим законы изменения Qy и Mz на участках АС и СВ балки.
На участке АС (0
На участке СВ (а
Из полученных выражений видно, что поперечная сила на участках АС и СВ имеет постоянное значение, а в точке С имеет скачок, равный Р. Изгибающие моменты изменяются по линейным законам, при этом в точках А и В Mz = 0, а в точке С Mz = Pab //. Эпюры Qy и Mz показаны на рис. 7.14.
Пример 7.2. Построим эпюры Qy и Mz для балки, нагруженной сосредоточенным моментом М (рис. 7.15).
Независимо от места приложения момента опорные реакции будут равны по величине и противоположны по направлению:
На участке АС (0 имеем:
На участке СВ (а имеем:
Из полученных выражений видно, что поперечная сила на обоих участках имеет одно и то же постоянное значение, а изгибающие моменты изменяются по линейным законам, при этом в точках А и В Mz = 0. В точке С изгибающий момент имеет различные значения слева и справа:
При этом на эпюре Mz имеется скачок, равный величине приложенного момента М. Эпюры Qy и Mz показаны на рис. 7.15.
Пример 7.3. Построим эпюры Qy и Mz для балки, показанной на рис. 7.16.
В силу симметрии нагрузки относительно середины балки опорные реакции равны между собой:
Выражения для поперечной силы и изгибающего момента в произвольном сечении х балки имеют следующий вид:
Таким образом, поперечная сила изменяется по длине балки по линейному закону, а изгибающий момент — по закону квадратной параболы.
Рис. 7.16
На опоре А балки Q = ql/2, Mz = 0, а на опоре В Qy = —ql/2, М = 0. В середине пролета при л: = 1/2 имеем:
Эпюры Q и Mz показаны на рис. 7.16.
Приведем общие выводы, которые можно сделать на основе дифференциальных соотношений (7.4) и рассмотренных выше примеров.
- 1. На участках балки, где отсутствует распределенная нагрузка q, поперечная сила Qy имеет постоянное значение, а изгибающий момент Mz изменяется по линейному закону.
- 2. На участках балки, где приложена равномерно распределенная нагрузка q, поперечная сила Qy изменяется по линейному закону, а изгибающий момент Mz — по закону квадратной параболы, обращенной выпуклостью в сторону действия нагрузки q.
- 3. В сечениях балки, где поперечная сила Qy равна нулю, изгибающий момент Mz может иметь экстремум.
- 4. В точке приложения сосредоточенной силы (рис. 7.14) на эпюре Qy имеется скачок, равный по величине приложенной в этой точке силе, а на эпюре Mz — излом в сторону действия силы.
- 5. В точке приложения сосредоточенного момента М на эпюре Mz имеется скачок, равный по величине приложенному моменту.
Эпюры Qy и Mz можно построить двумя способами.
Первый способ. Составляют аналитические выражения Qy(x) и Mz(x) для каждого участка балки, где они являются непрерывными функциями. Далее строят графики этих функции по участкам.
Второй способ. Вычисляют значения Qy и Mz в характерных сечениях балки, являющихся границами участков непрерывности внутренних усилий.
Если в каких-либо сечениях внутренние усилия имеют скачок, то определяют значения усилий слева и справа от этих сечений. Вычисленные значения ординат откладывают перпендикулярно к оси балки и полученные точки соединяют соответствующими линиями, используя дифференциальные зависимости (7.4) и (7.5) и сделанные выше выводы.
Эпюры заштриховываются прямыми линиями, перпендикулярными к оси балки, и указываются знаки внутренних усилий.
Рассмотрим примеры построения эпюр Qy и Mz для более сложных случаев нагружения.
Пример 7.4. Установим законы изменения Qy и Mz по длине консольной балки, изображенной на рис. 7.17, а, и построим эпюры этих величин.
Определим опорные реакции в жесткой заделке.
Балка имеет два участка с различными законами изменения внутренних усилий. Определим законы изменения Qy(x) и Mz(x) в пределах каждого из участков.
Рис. 7.17
Рис. 7.18
Участок АС (0
Проведем сечение в пределах первого участка на расстоянии л; от левого конца, отбросим мысленно правую часть балки и рассмотрим равновесие левой части под действием нагрузок и внутренних усилий в сечении (рис. 7.18, а).
Уравнения равновесия дают:
Определим значения Mz в начале и в конце участка:
х = О, М = —10 кНм (растянуты верхние волокна балки);
В пределах первого участка поперечная сила имеет постоянное значение, а изгибающий момент изменяется по линейному закону.
Участок СВ (2 м х
Проведем сечение в пределах второго участка (рис. 7.18, б), отбросим левую часть балки и рассмотрим равновесие правой части:
Отложим ординаты Qy и Mz, соответствующие началу и концу участков балки, перпендикулярно к ее оси и соединим полученные точки прямыми линиями. На втором участке поперечная сила отсутствует, а изгибающий момент имеет постоянное значение.
Эпюры Qy и Mz приведены на рис. 7.17, б, в.
Пример 7.5. Для консольной балки, изображенной на рис. 7.19, а, установим законы изменения Qy(x) и Mz(x) по длине балки и построим эпюры этих величин.
Определим опорные реакции в заделке В:
Отметим, что предварительное определение опорных реакций в заделке не обязательно. Определим законы изменения поперечной силы и изгибающего момента в пределах каждого из двух участков.
Участок АС (0 х 1 м)
Рассмотрим равновесие левой части балки (рис. 7.20, а)
Участок СВ (1м
Отбросим правую часть балки вместе с заделкой и рассмотрим равновесие оставшейся левой части (рис. 7.20, б):
Рис. 7.19
Рис. 7.20
Вычислим значения Q и Mz в начале и в конце участка:
В пределах первого участка поперечная сила имеет постоянное значение, а изгибающий момент изменяется по линейному закону. В пределах второго участка Qy изменяется по линейному закону, a Mz — по закону квадратной параболы.
В пределах второго участка поперечная сила обращается в нуль. Определим координату сечения, где Q = 0, и вычислим экстремальное значение момента Мтах:
Эпюры Qy и Mz приведены на рис. 7.19, б, в.
В сечении, где приложен сосредоточенный момент М, на эпюре Mz имеет место скачок, равный по величине приложенному моменту 5 кНм. Значения Qy и Mz в заделке равны по величине вычисленным ранее опорным реакциям.
Пример 7.6. Для однопролетной балки, изображенной на рис. 7.21, а, построим эпюры Qy и Mz.
Рис. 7.21
Расчет шарнирно опертых балок надо начинать с определения опорных реакций:
Вычислим значения Qy и Mz в характерных сечениях балки:
Эпюры Q и Mz приведены на рис. 7.21, б, в.
Пример 7.7. Для шарнирно опертой балки с консолью (рис. 7.22, а) определим значения Qy и Mz в характерных сечениях и построим эпюры этих величин.
Рис. 7.22
Определим опорные реакции:
Вычислим значения ^иМ^в характерных сечениях балки:
В пределах второго и третьего участков поперечная сила имеет постоянное значение, а в сечении В имеет скачок на величину опорной реакции RB. Изгибающий момент изменяется по линейному закону.
В пределах участка с распределенной нагрузкой изгибающий момент изменяется по закону квадратной параболы, а поперечная сила — по линейному закону. Установим положение сечения, где поперечная сила обращается в нуль, и вычислим экстремальное значение момента Мтах. Из подобия треугольников на эпюре Q получим:
Эпюры Qy и Mz приведены на рис. 7.22, б, в.
Пример 7.8. Для консольной балки, изображенной на рис. 7.23, а, вычислим значения Qy и Mz в характерных сечениях и построим их эпюры.
Определение Qy и Mz начнем со свободного конца балки:
х = 5 м, Qy= Mz = 0.
Внутренние усилия равны нулю, поскольку на свободном конце отсутствуют сосредоточенные нагрузки:
Рис. 7.23
Поперечная сила в пределах обоих участков балки изменяется по линейному закону, а изгибающий момент — по закону квадратной параболы. На свободном конце Q = 0 и касательная к эпюре Mz должна быть параллельна оси балки (поскольку М — 0, она совпадает с осью балки).
В пределах первого участка поперечная сила обращается в нуль. Из подобия треугольников на эпюре Qy определим координату сечения х0, где поперечная сила обращается в нуль, и для этого сечения определим величину экстремального изгибающего момента Mmin:
Эпюры Q и Mz приведены на рис. 7.23, б, в.
Пример 7.9. Для балки с промежуточным шарниром (рис. 7.24, а) построим эпюры Qy и Mz.
Данная балка является статически определимой, поскольку для определения трех опорных реакций RA, МА и Rc можно составить два обычных уравнения равновесия и дополнительное уравнение ^Мв = 0 для левой или правой части балки.
Рис. 7.24
Более удобным является расчет с помощью так называемой поэтажной схемы. Разрежем мысленно балку по промежуточному шарниру В. При этом выявляется характер взаимодействия балок Л В и ВС. Балка ВС не может работать самостоятельно и опирается на несущую балку Л В.
Вначале производится расчет несомой балки ВС, имеющей условную шарнирную опору в сечении В (рис. 7.24, б). Определяем опорные реакции:
Внутренние усилия в характерных сечениях балки ВС равны:
Расчет несущей балки ЛВ надо произвести на действие приложенной к ней распределенной нагрузки и силы, равной по величине условной опорной реакции RB и направленной в противоположную сторону (рис. 7.24, в). Внутренние усилия равны:
Эпюры Qy и Mz приведены на рис. 7.24, г. Поскольку в шарнире В не приложено сосредоточенных сил, на эпюре Qy нет скачка, а на эпюре Mz сопряжение линий является плавным.
Пример 7.10. Для консольного ломаного стержня (рис. 7.25, а) построим эпюры внутренних усилий N, 0, М.
Вычисление усилий для консольных балок и ломаных стержней удобно начинать со свободного конца. При этом не требуется предварительно определять опорные реакции.
Вычислим значения N, 0 и М в характерных сечениях стержня.
Участок АВ
Сечение А: N = 0, 0 = 0, М = 50 кНм
(растянуты нижние волокна).
Сечение В: N= 0, 0 = 20 • 2 = 40 кН,
М= 50 — 20 • 2 • 1 = 10 кНм (растянуты нижние волокна).
Участок ВС
Сечение В: N= — 20 • 2 = -40 кН (сжатие), 0 = 0,
М = 10 кНм (растянуты внутренние волокна).
Сечение С: N = -40 кН, 0 = 10 1,5 = 15 кН,
М= 10 — 10 • 1,5 • 0,75 = -1,25 кНм (растянуты внешние волокна).
Участок CD
Сечение С: N= -40 кН, 0 = 10 1,5 — 40 = -25 кН,
М = —1,25 кНм (растянуты внешние волокна).
M= 10 — 10 • 1,5 • 2,25 + 40 • 1,5 = 36,25 кНм (растянуты внутренние волокна).
Рис. 7.25
В пределах участков ЛВ и ВС поперечная сила изменяется по линейному закону, а изгибающий момент — по закону квадратной параболы, обращенной выпуклостью в сторону действия распределенной нагрузки. В пределах участка CD поперечная сила имеет постоянное значение, а изгибающий момент изменяется по линейном закону.
Эпюры N, Q и М приведены на рис. 7.25, б, в, г.
Проверим равновесие жесткого узла В. Для этого мысленно вырежем этот узел и приложим к нему внутренние усилия, действующие в поперечных сечениях горизонтального и вертикального стержней (рис. 7.25, д). Очевидно, что уравнения статики
2X = 0, 2^= 0 и J]МВ = 0 выполняются. Следовательно, узел В находится в равновесии.
Пример 7.11. Для стержня с криволинейным участком в виде четверти окружности (рис. 7.27, а) построим эпюры внутренних усилий N, Q и М.
Определим опорные реакции:
Рис. 7.26
Определим с помощью метода сечений законы изменения внутренних усилий на криволинейном участке (рис. 7.26). Приравнивая к нулю сумму проекций всех сил по направлению нормали и касательной к сечению, а также сумму моментов относительно центра тяжести сечения, получим:
Последовательно вычисляем:
Вычислим значения внутренних усилий в характерных сечениях горизонтального участка АС.
Откладывая вычисленные значения в рассмотренных сечениях перпендикулярно к оси стержня и соединяя полученные точки, построим эпюры внутренних усилий N, Q и М. Эти эпюры приведены на рис. 7.27, б, в, г.
Рис. 7.27
Поперечная сила Q на прямолинейном участке АС обращается в нуль в сечении на расстоянии х0 от точки А. В этом сечении изгибающий момент принимает экстремальное значение. Из подобия треугольников на эпюре Q определим
Вычислим экстремальное значение изгибающего момента:
Пример 7.12. Для балки с наклонным участком (рис. 7.28, а) построим эпюры N, Qm М.
Определим опорные реакции:
При определении продольной и поперечной сил в пределах наклонного участка надо нагрузку и опорные реакции проектировать на ось стержня и на нормаль к оси.
Составив уравнения равновесия участка стержня в пределах О х 3 м (рис. 7.28, д), находим:
Определение N и Q в пределах участка 3 м ё) производится аналогично:
Определение изгибающих моментов производится так же, как и для балок с горизонтальной осью. Эпюры N, Q, и М приведены на рис. 7.28, б, в, г.
Пример 7.13. Для рамы с шарнирными опорами (рис. 7.29, а) построим эпюры N, Q, и М.
Определяем величины опорных реакций:
Рис. 7.28
Рис. 7.29
Определяем внутренние усилия в характерных сечениях каждого участка рамы.
Участок AD
Сечение А: N = —RA = —30 кН (сжатие),
0 = —НА = —12 кН, М= 0.
Сечение D: N= -30 кН, Q = -12 кН,
М = —12 • 3 = —36 кНм (растянуты левые волокна).
Участок BE
Сечение В: N = —= -6 кН, 0 = 0, М = 0.
Сечение Е N = -6 кН, 0=4-3=12 кН,
М=-4-3- 1,5 = —18 кНм (растянуты правые волокна).
Участок СЕ
Сечение С: N= О, 0 = О, М=-6кНм
(растянуты верхние волокна).
Сечение D (слева): N= О, 0 = 0, М = -6 кНм.
Сечение D (справа): N = —НА = -12 кН, Q = RA = 30 кН,
М = —в — 12- 3 = —42 кНм.
Сечение F(слева): N= —12 кН, Q = 30 кН,
М= —42 + 30 1 = -12 кНм.
Сечение /’(справа): N= —12 кН, 0 = 30 — 36 = —6 кН,
М = -12 кНм.
Рис. 7.30
7V= —12 кН, 0 = —Rs = —6 кН,
М= -18 кНм.
Эпюры N, Q, и М приведены на рис. 7.29, б, в, г.
Вырежем мысленно узел D и покажем его равновесие под действием внутренних усилий в стержнях, сходящихся в узле (рис. 7.30). Нетрудно видеть, что узел находится в равновесии.
Источник