Построить эпюру крутящих моментов для бруса
Построение эпюр крутящих моментов
Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
Рис. 5.1
В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты Mk в поперечных сечениях различных участков вала неодинаковы.
На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.
При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. Mk примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).
В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент Mкр , а при свинчивании гайки – отрицательный.
Рис. 5.2
При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты МК связаны дифференциальной зависимостью
из которой вытекает следующая формула:
где – крутящий момент в начале участка.
Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение (МК = МКо = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре МК возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.
Рис. 5.3
На рис. 5.4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.
Рис. 5.4
В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.
Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.
Крутящий момент Mz1 в сечении I численно равен M1=200 нм и, согласно принятому правилу знаков, положителен.
Крутящий момент Mz2 в сечении II численно равен алгебраической сумме моментов M1 и M1, т.е. Mz2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.
Аналогичным образом вычисляется крутящий момент Mz3 в сечении III: Mz3 =200-300+500=400 нм.
Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.
Каждая ордината эп. Mk в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.
В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.
Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.
Пример 1.
Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4.1, а).
Рис.5.4.1
Решение.
Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.
1. Намечаем характерные сечения.
2. Определяем крутящий момент в каждом характерном сечении.
3. По найденным значениям строим эпюру (рис.5.4.1, б).
Пример 2.
Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: т (рис. 5.4.2).
Рис. 5.4.2. Построение эпюры внутренних крутящих моментов:
а – расчетная схема; б – первый участок, левая часть; в – второй участок, левая часть;
г – третий участок, правая часть; д – эпюра внутренних крутящих моментов
Решение.
В исходных сечениях 1–1; 2–2; 3–3 задаются положительными значениями внутренних крутящих моментов М1, М2, М3. Пусть .
Для первого участка (рис. 5.4.2, б):
ΣMk = M1 + M = 0;
M1 = –M = ml = const.
Для второго участка (рис. 5.4.2, в):
Для третьего участка (рис. 5.4.2, г):
Границы измерения параметра х3 в следующей системе координат:
Тогда
Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис. 5.4.2, д).
Пример 3.
На рис. 5.4.3 дан пример определения по методу сечений внутренних крутящих моментов по участкам и внизу (ри.5.4.3, с) изображена суммарная эпюра Мкр.
Рис.5.4.3. a) заданный стержень с нагрузкой; b) отсеченные части стержня;
с) эпюра крутящих моментов.
Решение.
В данном случае для консольного стержня вести вычисления удобно, идя справа налево, начав их с 3–го участка.
Участок 3(рис. 5.4.3, b). Неизвестный момент Mкр3 прикладываем к отсеченной части как положительный, после чего пишем условие равновесия отсеченной части:
Σотсеч mz3=Mкр3 +5=0; → Mкр3 = -5 тм, (0≤z3 ≤2).
Участок 2(рис. 5.4.3, b). Положение сечения фиксируем с помощью местной координаты z2 :
Σотсеч mz2= Mкр2 +3(4-z2 ) -15 +5=0; → Mкр2 =10 – 3(4-z2), (0≤z2≤2).
Точка z2 =0, Mкр2 =10 – 12= -2 тм.
Точка z2 =4, Mкр2 =10 – 0= 10 тм.
Участок 1(рис. 5.4.3, b):
Σотсеч mz1= Mкр1 +3∙4+5+5-15=0; → Mкр1 = -7 тм, (0≤z1 ≤2).
Найдем реактивный момент в заделке M0 из условия равновесия всего стержня Σmz =0, это дает M0 +3∙4+5+5-15=0 и M0 = -7 тм, что совпадает с Mкр1 , найденным на участке 1 по методу сечений. Этого конечно следовало ожидать, так как по существу реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник
Определение крутящих моментов и построение эпюры
Кручение стержня вызывается парами сил (сосредоточенными или распределенными), плоскость действия которых перпендикулярна продольной оси стержня. При кручении в поперечном сечении стержня возникает лишь один силовой фактор – крутящий момент Mк.
Согласно методу сечений величина и направление крутящего может быть найдены из уравнения равновесия моментов относительно оси стержня, составленного для оставленной части. То есть, крутящий момент в сечении численно равен алгебраической сумме моментов пар сил, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси стержня.
Правило знаков для крутящих моментов.
Крутящий момент считается положительным, если при взгляде на сечение со стороны внешней нормали он поворачивает сечение по ходу часовой стрелки и отрицательным — в противном случае.
При построение эпюры крутящих моментов положительные значения откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.
Это правило знаков условное и не совпадает с принятыми правилами знаков моментов, углов поворота в теоретической механике и математике, поскольку связано не с системой координат, а с видом деформации оставленной части.
Крутящий момент для сечения можно выразить так: $$M _к(x) = sum M _{кi} + sum int m _i(x)cdot dx$$
Распределенный крутящий момент m может быть постоянной или переменной интенсивности. Для постоянного распределенного момента m это выражение примет вид:
$$M _к(x) = sum M _{кi} + sum m _i(x)cdot (x- L_{mн}) — sum m _i(x)cdot (x- L_{mк})$$
где Lmн и Lmк – расстояние от начала координат до начала и до конца распределенного момента соответственно.
Дифференциальная зависимость внутренних усилий от распределенной нагрузки m:
dMк = m·dx
Общий порядок расчета и построения эпюры.
- Намечаем характерные сечения стержня.
- Определяем крутящий момент в каждом характерном сечении.
- По найденным значениям моментов строим эпюру.
Построение эпюр крутящих моментов (пример)
Построить эпюру крутящих моментов для жестко защемленного стержня
Пусть прямолинейный стержень нагружен внешними сосредоточенными крутящими моментами Mкв1=-30кН·м, Mкв2=50 кН·м, и распределенным моментом m1=10кН. Реакции левой опоры можно не определять, т.к. в этом примере можно ограничиться рассмотрением лишь сил, приложенных к правым оставленным частям (справа от сечений).
1. Число характерных сечений — 6
Для заданного консольного стержня вычисления удобно вести, идя справа налево, начав их с 1–го сечения.
2. Проведем сечение 1. Определим крутящий момент в текущем сечении:
Mк1= Mкв2= 50 кНм
3. Проведем сечение 2. Отбросим левую часть, заменим ее действие крутящим моментом Mк2 и составим уравнение равновесия в моментах относительно оси бруса. Из уравнения равновесия получаем выражение для крутящего момента в сечении 2:
Mк2 = Mк1 = Mкв2 = 50 кНм
3. Проведем сечение 3, отбрасываем левую часть, составляем уравнение равновесия и получаем:
Mк3 = Mкв2 – m1*4 = 50 – 10*4 = 10 кНм
4. Аналогично для сечения 4:
Mк4 = Mк3 = 10 кНм
5. Также для сечения 5:
Mк5= Mк4-Mкв1= 10 – 30 = -20 кНм
6. Для сечения 6:
Mк6= Mк5 =-20 кНм
7. По полученным значения строим эпюру крутящих моментов (см. рис.).
Скачок на левом конце эпюры дает величину опорного момента (реактивного момента в заделке) Mк6, так как реактивный момент – это внутреннее усилие, действующее в поперечном сечении, где соединены торец стержня и заделка.
Правила контроля правильности эпюр крутящих моментов
Для эпюр крутящих моментов характерны некоторые закономерности, знание которых позволяет оценить правильность построений.
- Эпюры крутящих моментов всегда прямолинейные.
- На участке, где нет распределенных моментов, эпюра Mк – прямая, параллельная оси; а на участке с распределенными моментами – наклонная прямая.
- Под точкой приложения сосредоточенного момента на эпюре Mк будет скачок на величину этого момента.
Дополнительно
Еще один вариант построения эпюры крутящих моментов с использованием компьютера найдете на этой странице.
Пример из пособия МИИТ Построение эпюры крутящих моментов (формат pdf).
метки: внутренние усилия,
кручение
Источник
Построение эпюр крутящих моментов
Крутящий момент в некотором сечении бруса равен сумме моментов всех внешних сил относительно продольной оси Z. Правило знаков для крутящего момента условно: можно считать крутящий момент положительным, если при взгляде со стороны сечения он направлен по часовой стрелке (или против) – рисунок 5.1.
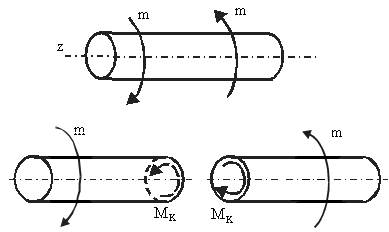
Рисунок 5.1 – Загружение бруса и внутренние усилия при кручении
Момент, передаваемый на вал от двигателя в установившемся режиме, уравновешивается реактивными моментами в шкивах, отбирающих мощность:
;
; (5.1)
Рисунок 5.2 – Загружение вала и построение эпюры крутящих моментов на участках методом сечений
Расчет вала со шкивами при изгибе с кручением подробно рассмотрен в §11.1.
§5.2 Кручение круглого стержня
Каждое сечение круглого стержня при кручении поворачивается как жёсткое целое только в своей плоскости (гипотеза плоских сечений). Методы теории упругости доказывают справедливость этой гипотезы для круглого и кольцевого сечений.
Рассмотрим элементарный участок стержня – цилиндр высотой dz при кручении (рисунок 5.3).
− элементарный угол закручивания оси стержня в пределах длины dz;
− угол сдвига цилиндрической поверхности радиуса r;
− относительный угол закручивания;
.
− закон Гука при сдвиге, ;
− касательные напряжения в поперечном сечении линейного изменяются по радиусу (рисунок 5.4).
;
− полярный момент инерции;
.
− полярный момент сопротивления.
Для круга (рисунок 5.5а):
; .
Для кольца (рисунок 5.5б):
; ; .
Для тонкостенной трубы (рисунок 5.5в):
, , ,
где − средний радиус.
, или
. (5.2)
− жёсткость бруса при кручении;
; (5.3)
.
Если в пределах участка длиной l крутящий момент и жёсткость бруса постоянны, то угол закручивания вала на длине участка liнаходят по формуле:
. (5.4)
Полный угол закручивания вала на нескольких участках равен сумме углов закручивания отдельных участков:
. (5.4а)
Условие жесткости при кручении имеет вид:
. (5.5)
. (5.6)
, где .
Условие прочности при кручении имеет вид:
. (5.7)
Потенциальная энергия при кручении находится по формуле:
; . (5.8)
§5.3 Понятие о кручении стержня прямоугольного сечения
При кручении стержня некруглого сечения гипотеза плоских сечений не выполняется (сечения депланируют), а расчётные формулы касательных напряжений сильно усложняются. Качественную картину удобно изображать потоком касательных напряжений (рисунок 5.6).
Во внешних углах , во внутренних углах (концентрация напряжений). Для прямоугольного сечения (рисунок 5.7) пользуются обычными формулами:
, (5.9)
, (5.10)
где , , (Беляев, Дарков). (5.11)
, , (Феодосьев, Александров).
Коэффициенты , , ( , , ) приведены в таблицах различных источников в зависимости от отношения сторон (таблица 5.1).
Таблица 5.1 – Коэффициенты для расчета на кручение бруса прямоугольного сечения
([1.11] Дарков А.В., табл. 6.1)
| 1,5 | 0,140 0,294 0,457 0,790 1,123 1,789 2,456 3,123 | 0,208 0,346 0,493 0,801 1,150 1,789 2,456 3,123 | 0,859 0,795 0,753 0,745 0,743 0,742 0,742 |
§5.4 Определение перемещений и напряжений в витых цилиндрических пружинах
Рассмотрим загружение осевыми растягивающими силами Р витой цилиндрической пружины, изображенной на рисунке 5.8.
Рисунок 5.8 – Загружение витой цилиндрической пружины растягивающей силой Р и внутренние усилия в сечении прутка
При можно считать вертикальное сечение прутка перпендикулярным к его криволинейной оси, тогда , .
Рисунок 5.9 – Касательные напряжения в сечении прутка пружины от среза и от кручения
— средние касательные напряжения от среза,
— касательные напряжения от крутящего момента (рисунок 5.9).
. (5.12)
При малых диаметрах прутка , тогда
. (5.12а)
Работа А статической силы P на перемещении равна
. (5.13)
Потенциальную энергию U деформации пружины найдём только от крутящих моментов:
, (5.14)
где , n − число рабочих витков пружины (не учитываются витка по концам пружины).
На основании закона сохранения энергии:
, ,
(5.15)
— формула полной осадки пружины.
Жёсткость пружины рассчитывают по формуле:
, . (5.16)
Формула для определения силы Р в пружине по величине ее полной осадки λ имеет вид:
. (5.17)
§5.5 Расчёт заклёпочных, болтовых и сварных соединений
1) Расчёт болтовых и заклёпочных соединений
Рассмотрим симметричный стык с двумя накладками (четное число плоскостей среза) – рисунок 5.10. Справочные данные по механическим характеристикам болтов даны в Приложении 3.
Все монтажные стыки стальных конструкций должны быть болтовыми [1.7].
Диаметр отверстий D под монтажные болты должен быть на 1÷3 мм больше диаметров болтов d: D-d = (1, 2, 3) мм.
Монтажные болты по ГОСТу выполняются для одних и тех же размеров для нескольких классов прочности, выбитых на головке (Приложение 3).
Классы прочности: .
Расчёт на прочность болтового стыка ведётся по трём состояниям:
1) Разрыв листов (рисунок 5.11а).
, (5.17)
(5.18)
где Fнт — “чистая” площадь нетто ослабленного сечения листа,
n – число болтов в одном поперечном ряду стыка (но не по зигзагу).
«Где тонко – там и рвётся».
.
2) Срез болтов (рисунок 5.11б)
; (5.19)
; (5.20)
— расчетное сопротивление болтов срезу для данного класса прочности (приложение 3),
n – полное число болтов в стыке,
m – число плоскостей среза для одного болта.
. (5.21)
3) Смятие болтов (рисунок 5.11б)
, (5.22)
, (5.22а)
— расчетное сопротивление смятию элементов, соединяемых болтами (Приложение 3).
; (5.23)
. (5.24)
Распределение напряжений смятия по диаметру, а также касательных напряжений среза по сечению отдельного болта (шпонки, заклепки) принимается равномерным, то есть без учета реальной концентрации напряжений (рисунок 5.12), что нашло хорошее подтверждение в практике эксплуатации данных соединений.
Несущая способность стыка равна минимальной допускаемой нагрузке из этих трёх условий прочности.
. (5.25)
В соединениях, где болты работают на отрыв, условие прочности составляется для ослабленного резьбой сечения:
. (5.26)
Значение площадей ослабленных резьбой сечений и расчётных сопротивлений болтов на срез Rbs и растяжение Rbt даны в таблице 58 СНиП 2.23.81* «Стальные конструкции» (см. Приложение 3).
2) Расчёт сварных соединений
Сварные соединения выполняются в заводских условиях, с контролем качества шва. Расчетная длина шва l уменьшается на 1см для учета непровара в конце шва.
Площадь углового сварного шва на срез вычисляется под углом 450 к катету (рисунок 5.14):
,
kf – катет сварного шва.
, (5.27)
, (5.28)
— расчетное сопротивление материала сварного шва на срез (Приложение 3).
Подберём минимальную длину накладок L из условия равнопрочности листов стыка и сварных швов.
, (5.29)
— расчетное сопротивление материала листа на растяжение (Приложение 3).
.
Длина накладок L подбирается из условия равнопрочности сварки на срез и основного металла листов на разрыв.
,
,
, (5.30)
, .
Полную длину накладок L стыка находим по формуле .
Расчёт сварного стыка без накладок (рисунок 5.15)
Длина стыкового сварного шва с учетом непровара (см),
, где t – наименьшая толщина соединяемых элементов.
, (5.31)
— расчетное сопротивление материала шва на растяжение и сжатие (Приложение 3).
, (5.32)
, (5.33)
где — несущая способность стыка из условия прочности листа.
. (5.34)
При надлежащем качестве шва и материала электрода сварной стык, как правило, прочнее основного металла.
Рисунок 5.15 – Стыковой сварной шов двух листов
Пример. Расчёт сварного заводского стыка прокатного двутавра I№30Б2 на накладках (ГОСТ 26020-83) – рисунок 5.16.
Рисунок 5.16 – Конструкция сварного заводского стыка прокатного двутавра на накладках
Дано: Балка I№30Б2, сталь С245.
Накладки 1: l1x b1x t1 = 480x180x10, катет сварных швов kf1 = 8 мм.
Накладки 2: l2x b2x t2 = 240x120x6, катет сварных швов kf2 = 5 мм.
Расчетное сопротивление срезу сварного шва для электрода Э42 Rwf = 180 МПа (1850 кгс/см2).
Рассчитать несущую способность стыка на изгиб и на срез и определить запас прочности стыка по сравнению с цельным сечением.
Решение
1) Выполняем расчет несущей способности цельного сечения.
Сталь С245, Ry = 240 МПа (2450 кгс/см2), Rs = 0,58Ry = 1420 кгс/см2.
I30Б2, h = 300, b = 140, d = 6, t = 10, JxI= 7293 см4, WxI= 487,8 см3, Sx0 =273,8см3.
Определяем допускаемые усилия для цельного сечения двутавра I30Б2.
[M]0 = Ry·WxI= 2450 кгс/см2·487,8 см3 = 11,95·105кгс·см = 11,95 тм.
[Q]0 = Rs·Jx·d/Sx0 = 1420 кгс/см2·7293см4·0,6см/273,8 см3 = 22700 кгс = 22,7 т.
2) Выполняем расчет несущей способности сварного стыка. В запас прочности рекомендуется рассчитывать отдельно горизонтальные накладки полок двутавра на изгибающий момент, а вертикальные накладки стенки — на срез.
Рассчитаем момент сопротивления сечения накладок горизонтальных накладок:
F1 = b1·t1 = 18·1 = 18 см2, h0 = h+t1 = 31 см,
,
.
[M]1 = Ry·Wx1 = 2450 кгс/см2 · 540,5 см3 = 13,24 · 105 кгс·см = 13,24 тм.
Рассчитаем площадь сечения вертикальных накладок
F2 = 2t2 · l2 = 2 · 0,6см · 24см = 28, 8 см2.
[Q]1 = Rs · F2 = 1420кгс/см2 · 28,8см2 = 40896 кгс = 40,9 т.
Рассчитаем усилия Т1, приходящиеся на один шов горизонтальных накладок.
,
Длина сварного шва горизонтальных накладок с одной стороны стыка:
lш1 = 215 — 10 = 205 мм ≈ 20 см.
Напряжения в сварном шве горизонтальной накладки:
.
[T]1 = Rwf · 0,7·kf1·lш1 = 1850кгс/см2·0,7·0,8см·20см = 20720 кгс = 20,72 т
[M]2 = [T]1·2h = 20,72т·2·0,3м = 12,43 тм
Рассчитаем усилия Т2, приходящиеся на один шов вертикальной накладки.
Длина сварного шва вертикальной накладки с одной стороны стыка:
lш2 = l2-10 = 240-10 = 230 мм.
Напряжения в сварном шве вертикальной накладки:
[T]2 = Rwf · 0,7 · kf2 · lш2 = 1850кгс/см2 · 0,7 · 0,5см · 23см = 14900 кгс = 14,9 т
[Q]2 = 2[T]2 = 2·14,9т = 29,8 т
Несущая способность стыка на изгиб определяется прочностью на срез сварных швов горизонтальных накладок:
.
Запас прочности на изгиб .
Несущая способность стыка на срез определяется прочностью на срез сварных швов вертикальных накладок:
.
Запас прочности на срез .
Ответ: минимальный коэффициент запаса прочности стыка из условия прочности на изгиб составил nmin = 1,04.
Источник