Реши уравнение и построй дом
Калькулятор онлайн — Решение квадратного уравнения (с подробным решением)
С помощью этой математической программы вы можете решить квадратное уравнение.
Программа не только даёт ответ задачи, но и отображает процесс решения двумя способами:
— с помощью дискриминанта
— с помощью теоремы Виета (если возможно).
Причём, ответ выводится точный, а не приближенный.
Например, для уравнения (81x^2-16x-1=0) ответ выводится в такой форме:
$$ x_1 = frac{8+sqrt{145}}{81}, quad x_2 = frac{8-sqrt{145}}{81} $$
а не в такой: ( x_1 = 0,247; quad x_2 = -0,05 )
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.
Правила ввода квадратного многочлена
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5z +1/7z^2
Результат: ( 3frac{1}{3} — 5frac{6}{5} z + frac{1}{7}z^2 )
При вводе выражения можно использовать скобки. В этом случае при решении квадратного уравнения введённое выражение сначала упрощается.
Например: 1/2(y-1)(y+1)-(5y-10&1/2)
Примеры подробного решения >>
Наши игры, головоломки, эмуляторы:
Квадратное уравнение и его корни. Неполные квадратные уравнения
Каждое из уравнений
( -x^2+6x+1{,}4=0, quad 8x^2-7x=0, quad x^2-frac{4}{9}=0 )
имеет вид
( ax^2+bx+c=0, )
где x — переменная, a, b и c — числа.
В первом уравнении a = -1, b = 6 и c = 1,4, во втором a = 8, b = —7 и c = 0, в третьем a = 1, b = 0 и c = 4/9. Такие уравнения
называют квадратными уравнениями.
Определение.
Квадратным уравнением называется уравнение вида ax2+bx+c=0, где x — переменная, a, b и c — некоторые числа,
причём ( a neq 0 ).
Числа a, b и c — коэффициенты квадратного уравнения. Число a называют первым коэффициентом, число b — вторым коэффициентом и
число c — свободным членом.
В каждом из уравнений вида ax2+bx+c=0, где ( a neq 0 ), наибольшая степень переменной x — квадрат. Отсюда и название:
квадратное уравнение.
Заметим, что квадратное уравнение называют ещё уравнением второй степени, так как его левая часть есть многочлен второй степени.
Квадратное уравнение, в котором коэффициент при x2 равен 1, называют приведённым квадратным уравнением.
Например, приведёнными квадратными уравнениями являются уравнения
( x^2-11x+30=0, quad x^2-6x=0, quad x^2-8=0 )
Если в квадратном уравнении ax2+bx+c=0 хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называют
неполным квадратным уравнением. Так, уравнения -2×2+7=0, 3×2-10x=0, -4×2=0 — неполные
квадратные уравнения. В первом из них b=0, во втором c=0, в третьем b=0 и c=0.
Неполные квадратные уравнения бывают трёх видов:
1) ax2+c=0, где ( c neq 0 );
2) ax2+bx=0, где ( b neq 0 );
3) ax2=0.
Рассмотрим решение уравнений каждого из этих видов.
Для решения неполного квадратного уравнения вида ax2+c=0 при ( c neq 0 ) переносят его свободный член в правую часть
и делят обе части уравнения на a:
( x^2 = -frac{c}{a} Rightarrow x_{1,2} = pm sqrt{ -frac{c}{a}} )
Так как ( c neq 0 ), то ( -frac{c}{a} neq 0 )
Если ( -frac{c}{a}>0 ), то уравнение имеет два корня.
Если ( -frac{c}{a}Для решения неполного квадратного уравнения вида ax2+bx=0 при ( b neq 0 ) раскладывают его левую часть на множители
и получают уравнение
( x(ax+b)=0 Rightarrow left{ begin{array}{l} x=0 \ ax+b=0 end{array} right. Rightarrow left{ begin{array}{l} x=0 \ x=-frac{b}{a} end{array} right. )
Значит, неполное квадратное уравнение вида ax2+bx=0 при ( b neq 0 ) всегда имеет два корня.
Неполное квадратное уравнение вида ax2=0 равносильно уравнению x2=0 и поэтому имеет единственный корень 0.
Формула корней квадратного уравнения
Рассмотрим теперь, как решают квадратные уравнения, в которых оба коэффициента при неизвестных и свободный член отличны от нуля.
Решим квадратне уравнение в общем виде и в результате получим формулу корней. Затем эту формулу можно будет применять при решении любого
квадратного уравнения.
Решим квадратное уравнение ax2+bx+c=0
Разделив обе его части на a, получим равносильное ему приведённое квадратное уравнение
( x^2+frac{b}{a}x +frac{c}{a}=0 )
Преобразуем это уравнение, выделив квадрат двучлена:
( x^2+2x cdot frac{b}{2a}+left( frac{b}{2a}right)^2- left( frac{b}{2a}right)^2 + frac{c}{a} = 0 Rightarrow )
( x^2+2x cdot frac{b}{2a}+left( frac{b}{2a}right)^2 = left( frac{b}{2a}right)^2 — frac{c}{a} Rightarrow )
( left( x+frac{b}{2a}right)^2 = frac{b^2}{4a^2} — frac{c}{a} Rightarrow left( x+frac{b}{2a}right)^2 = frac{b^2-4ac}{4a^2} Rightarrow )
( x+frac{b}{2a} = pm sqrt{ frac{b^2-4ac}{4a^2} } Rightarrow x = -frac{b}{2a} + frac{ pm sqrt{b^2-4ac} }{2a} Rightarrow )
( x = frac{ -b pm sqrt{b^2-4ac} }{2a} )
Подкоренное выражение называют дискриминантом квадратного уравнения ax2+bx+c=0 («дискриминант» по латыни —
различитель). Его обозначают буквой D, т.е.
( D = b^2-4ac )
Теперь, используя обозначение дискриминанта, перепишем формулу для корней квадратного уравнения:
( x_{1,2} = frac{ -b pm sqrt{D} }{2a} ), где ( D= b^2-4ac )
Очевидно, что:
1) Если D>0, то квадратное уравнение имеет два корня.
2) Если D=0, то квадратное уравнение имеет один корень ( x=-frac{b}{2a} ).
3) Если DТаким образом, в зависимости от значения дискриминанта квадратное уравнение может иметь два корня (при D > 0), один корень
(при D = 0) или не иметь корней (при D При решении квадратного уравнения по данной формуле целесообразно поступать следующим образом:
1) вычислить дискриминант и сравнить его с нулём;
2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней, если дискриминант отрицателен, то записать,
что корней нет.
Теорема Виета
Приведённое квадратное уравнение ax2-7x+10=0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10.
Мы видим, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному
члену. Таким свойством обладает любое приведённое квадратное уравнение, имеющее корни.
Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней
равно свободному члену.
Т.е. теорема Виета утверждает, что корни x1 и x2 приведённого квадратного уравнения x2+px+q=0
обладают свойством:
( left{ begin{array}{l} x_1+x_2=-p \ x_1 cdot x_2=q end{array} right. )
Источник
Калькулятор онлайн — Решение показательных уравнений
Этот математический калькулятор онлайн поможет вам решить показательное уравнение.
Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное
решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Вы можете посмотреть теорию о показательной функции и
общие методы решения показательных уравнений.
Примеры подробного решения >>
Введите показательное уравнение
Наши игры, головоломки, эмуляторы:
Показательная функция, её свойства и график
Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) an am = an+m
2) ( frac{a^n}{a^m} = a^{n-m} )
3) (an)m = anm
4) (ab)n = an bn
5) ( left( frac{a}{b} right)^n = frac{a^n}{b^n} )
6) an > 0
7) an > 1, если a > 1, n > 0
8) anm, если a > 1, n
9) an > am, если 0
В практике часто используются функции вида y = ax, где a — заданное положительное число, x — переменная.
Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является
показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = ax, где а — заданное число, a > 0, ( a neq 1)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень ax где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение ax = b, где а > 0, ( a neq 1), не имеет корней,
если ( b leqslant 0), и имеет корень при любом b > 0.
3) Показательная функция у = ax является возрастающей на множестве всех действительных чисел, если a > 1, и
убывающей, если 0
Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = ax при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = ax при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = ax при 0
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является
горизонтальной асимптотой графика.
Если х 

Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения ax = ab где а > 0, ( a neq 1),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, ( a neq 1) равны
тогда и только тогда, когда равны их показатели.
Решить уравнение 23x • 3x = 576
Так как 23x = (23)x = 8x, 576 = 242, то уравнение можно записать в виде
8x • 3x = 242, или в виде 24x = 242, откуда х = 2.
Ответ х = 2
Решить уравнение 3х + 1 — 2 • 3x — 2 = 25
Вынося в левой части за скобки общий множитель 3х — 2, получаем 3х — 2(33 — 2) = 25,
3х — 2 • 25 = 25,
откуда 3х — 2 = 1, x — 2 = 0, x = 2
Ответ х = 2
Решить уравнение 3х = 7х
Так как ( 7^x neq 0 ) , то уравнение можно записать в виде ( frac{3^x}{7^x} = 1 ), откуда ( left( frac{3}{7} right) ^x = 1 ), х = 0
Ответ х = 0
Решить уравнение 9х — 4 • 3х — 45 = 0
Заменой 3х = t данное уравнение сводится к квадратному уравнению t2 — 4t — 45 = 0. Решая это уравнение,
находим его корни: t1 = 9, t2 = -5, откуда 3х = 9, 3х = -5.
Уравнение 3х = 9 имеет корень х = 2, а уравнение 3х = -5 не имеет корней, так как показательная функция не
может принимать отрицательные значения.
Ответ х = 2
Решить уравнение 3 • 2х + 1 + 2 • 5x — 2 = 5х + 2х — 2
Запишем уравнение в виде
3 • 2х + 1 — 2x — 2 = 5х — 2 • 5х — 2, откуда
2х — 2 (3 • 23 — 1) = 5х — 2( 5 2 — 2 )
2х — 2 • 23 = 5х — 2• 23
( left( frac{2}{5} right) ^{x-2} = 1 )
x — 2 = 0
Ответ х = 2
Решить уравнение 3|х — 1| = 3|х + 3|
Так как 3 > 0, ( 3 neq 1), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1)2 = (х + 3)2, откуда
х2 — 2х + 1 = х2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
Источник
«Решение уравнений» — Яндекс.Кью
Dum spiro, spero.
Любопытство — не порок, а очень даже полезная вещь… · 19 февраля 2019
Сначала раскрываем скобки:
24х + 48 = 6х — 24
Далее переносим х влево, а числа вправо, меняя знаки:
24х — 6х = -24 — 48
Вычисляем:
18х = -72
х = -4
Проверяем подстановкой:
24 (-4+2) = 6 (-4-4)
24 * (-2) = 6 * (-8)
-48 = -48
Ответ: х = -4. Читать далее
Имею естественно научное образование, в юношестве прикипел к литературе, сейчас… · 5 марта 2019
sinx⋅tgx−(−3√)sinx=0
Разложим на множители
sinx(tgx−(−3√))=0
sinx=0, tgx−(−3√)=0
sinx=0
x=180° n
x=arctga+180n, x=arctga+πk,
tgx=−√3
x = −60°+180n°
x=180° n
x = −60° +180° n, n ∈ Z Читать далее
Комментировать ответ…Комментировать…
Не перестаю узнавать новое. Люблю путешествия и все с этим связанное. Много лет… · 25 декабря 2018
Чтобы решить это уравнение, сначала нужно раскрыть скобки:
8х-112=56
А затем сгруппировать члены уравнения: в одну сторону те, которые содержат неизвестную, а в другую.
8х=56+112
8х=168
х=21 Читать далее
Комментировать ответ…Комментировать…
Во-первых, [a] — это не «наибольшая целая часть». Это просто целая часть, которая определяется как наибольшее целое число, не превышающее a. Например [1] = 1, [1.5] = 1, [1.999] = 1, [2] = 2. Теперь к решению.
Для начала решим уравнение попроще : x + 2x = 2018. его решение x =… Читать далее
Комментировать ответ…Комментировать…
12х2+3х=0 (2 после х — степень)
Выносим общий множитель за скобку.
3х(4х+1)=0
Уравнение равно нулю, когда один из множителей равен 0, то есть раскладываем получившееся уравнение на 2 части.
3х=0 4х+1=0
х=0 4х=-1
х=-14
Ответ: 0, -14 Читать далее
Комментировать ответ…Комментировать…
Нравится познавать и наслаждаться этим миром · 23 мая 2019
Построим графики функций левой и правой части равенства: f(x) = x^2 и f(x) = x — 4 соответсвенно. Полученные графики не пересекаются, т.е. не имеют общах точек. Значит данное уравнение не имеет действительных решений. Читать далее
Комментировать ответ…Комментировать…
Такая задача сводится к нахождению точек разрыва функции. Зная эти точки, можно так же найти и интервалы, на которых функция непрерывна.
Функция непрерывна в точке х, если предел функции в данной точке равен значению функции в этой точке.
Определение детализируется в следующих… Читать далее
Комментировать ответ…Комментировать…
Все мы проходили в школе задачи на вероятность — будет снег, не будет, и вероятность этого события.
А что, если я захочу узнать вероятность события, что 27 марта будет 15 градусов? То бишь… Развернуть
Ну, если совсем по-честному, то эту задачу никто точно не решил, не только вы в школе.
Для того, чтобы посчитать вероятность какого-то одного исхода эксперимента нужно знать функцию распределения — функцию, которая, собственно, и показывает вероятности различных исходов. В школе как… Читать далее
Комментировать ответ…Комментировать…
Определи массовую долю (в %) кремния в техническом кремнии, если при сжигании 6,63 г технического кремния образовалось 8,78 г SiO2.
(Ответ и промежуточные расчёты округляй с точностью до сотых.)
Определи массовую долю (в %) кремния в техническом кремнии, если при сжигании 6,63 г технического кремния образовалось 8,78 г SiO2.
(Ответ и промежуточные расчёты округляй с точностью до сотых.)
Реакция горения кремния Si + O2 = SiO2
Если SiO2 образовалось 8,78 г, его молярная… Читать далее
Комментировать ответ…Комментировать…
Источник
ОГЭ, Математика. Числа и вычисления: Задача №DD429C | Ответ-Готов
ÐадаÑа â447 из 458 |
Ðа плане изобÑажено домоÑ
озÑйÑÑво по адÑеÑÑ: СÐТ «ÐÑибоÑ», 2-Ñ ÐиниÑ, д. 26 (ÑÑоÑона каждой клеÑки на плане Ñавна 2 м). УÑаÑÑок Ð¸Ð¼ÐµÐµÑ Ð¿ÑÑмоÑголÑнÑÑ ÑоÑмÑ. ÐÑезд и вÑезд оÑÑÑеÑÑвлÑÑÑÑÑ ÑеÑез единÑÑвеннÑе воÑоÑа.
ÐÑи вÑ
оде на ÑÑаÑÑок ÑпÑава Ð¾Ñ Ð²Ð¾ÑÐ¾Ñ Ð½Ð°Ñ
одиÑÑÑ Ð³Ð°Ñаж, а Ñлева в ÑÐ³Ð»Ñ ÑÑаÑÑка ÑаÑположен ÑаÑай, оÑмеÑеннÑй на плане ÑиÑÑой 1. ÐлоÑадÑ, занÑÑÐ°Ñ ÑаÑаем, Ñавна 24 кв. м.
Ðилой дом наÑ
одиÑÑÑ Ð² глÑбине ÑеÑÑиÑоÑии и обознаÑен на плане ÑиÑÑой 6. Ðомимо гаÑажа, жилого дома и ÑаÑаÑ, на ÑÑаÑÑке имееÑÑÑ Ð»ÐµÑнÑÑ Ð±ÐµÑедка, ÑаÑÐ¿Ð¾Ð»Ð¾Ð¶ÐµÐ½Ð½Ð°Ñ Ð½Ð°Ð¿ÑоÑив вÑ
ода в дом, и мангал ÑÑдом Ñ Ð½ÐµÐ¹. Ðа ÑÑаÑÑке Ñакже ÑаÑÑÑÑ ÐµÐ»Ð¸. Ð ÑенÑÑе ÑÑаÑÑка ÑаÑположен ÑвеÑник.
ÐÑе доÑожки внÑÑÑи ÑÑаÑÑка имеÑÑ ÑиÑÐ¸Ð½Ñ 1 м и вÑмоÑÐµÐ½Ñ ÑÑоÑÑаÑной плиÑкой ÑазмеÑом 50cм x 50cм. ÐеÑед гаÑажом и Ð¼ÐµÐ¶Ð´Ñ Ð´Ð¾Ð¼Ð¾Ð¼ и беÑедкой имеÑÑÑÑ Ð¿Ð»Ð¾Ñадки плоÑадÑÑ 40 и 16 кв. м ÑооÑвеÑÑÑвенно, вÑмоÑеннÑе Ñакой же плиÑкой.
РдомоÑ
озÑйÑÑÐ²Ñ Ð¿Ð¾Ð´Ð²ÐµÐ´ÐµÐ½Ð¾ ÑлекÑÑиÑеÑÑво. ÐмееÑÑÑ Ð¼Ð°Ð³Ð¸ÑÑÑалÑное газоÑнабжение.
ÐайдиÑе ÑаÑÑÑоÑние Ð¾Ñ Ð³Ð°Ñажа до жилого дома (ÑаÑÑÑоÑние Ð¼ÐµÐ¶Ð´Ñ Ð´Ð²ÑÐ¼Ñ Ð±Ð»Ð¸Ð¶Ð°Ð¹Ñими ÑоÑками по пÑÑмой) в меÑÑаÑ
.
ТÑоÑÑаÑÐ½Ð°Ñ Ð¿Ð»Ð¸Ñка пÑодаÑÑÑÑ Ð² ÑÐ¿Ð°ÐºÐ¾Ð²ÐºÐ°Ñ Ð¿Ð¾ 8 ÑÑÑк. СколÑко Ñпаковок плиÑки понадобилоÑÑ, ÑÑÐ¾Ð±Ñ Ð²ÑложиÑÑ ÑолÑко доÑожки?
ÐÐ»Ñ Ð¾Ð±ÑекÑов, ÑказаннÑÑ Ð² ÑаблиÑе, опÑеделиÑе, какими ÑиÑÑами они обознаÑÐµÐ½Ñ Ð½Ð° плане. ÐаполниÑе ÑаблиÑÑ, в бланк оÑвеÑов пеÑенеÑиÑе поÑледоваÑелÑноÑÑÑ ÑеÑÑÑÑÑ ÑиÑÑ Ð±ÐµÐ· пÑобелов, запÑÑÑÑ Ð¸ дÑÑÐ³Ð¸Ñ Ð´Ð¾Ð¿Ð¾Ð»Ð½Ð¸ÑелÑнÑÑ Ñимволов.
| ÐбÑекÑÑ | беÑедка | ели | гаÑаж | мангал |
| ЦиÑÑÑ |
ÐÐ»Ñ Ð¾Ð±ÑекÑов, ÑказаннÑÑ Ð² ÑаблиÑе, опÑеделиÑе, какими ÑиÑÑами они обознаÑÐµÐ½Ñ Ð½Ð° плане. ÐаполниÑе ÑаблиÑÑ, в бланк оÑвеÑов пеÑенеÑиÑе поÑледоваÑелÑноÑÑÑ ÑеÑÑÑÑÑ ÑиÑÑ Ð±ÐµÐ· пÑобелов, запÑÑÑÑ Ð¸ дÑÑÐ³Ð¸Ñ Ð´Ð¾Ð¿Ð¾Ð»Ð½Ð¸ÑелÑнÑÑ Ñимволов.
| ÐбÑекÑÑ | ÑвеÑник | гаÑаж | мангал | беÑедка |
| ЦиÑÑÑ |
ТÑоÑÑаÑÐ½Ð°Ñ Ð¿Ð»Ð¸Ñка пÑодаÑÑÑÑ Ð² ÑÐ¿Ð°ÐºÐ¾Ð²ÐºÐ°Ñ , ÑаÑÑÑиÑаннÑÑ Ð½Ð° 3,5 кв. м. СколÑко Ñпаковок Ñакой плиÑки понадобилоÑÑ, ÑÑÐ¾Ð±Ñ Ð²ÑложиÑÑ Ð²Ñе доÑожки и обе плоÑадки?
ÐайдиÑе плоÑадÑ, коÑоÑÑÑ Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ Ð¶Ð¸Ð»Ð¾Ð¹ дом. ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе в квадÑаÑнÑÑ Ð¼ÐµÑÑÐ°Ñ .
СколÑко пÑоÑенÑов плоÑади вÑего ÑÑаÑÑка Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ ÑаÑай?
ÐайдиÑе плоÑадÑ, коÑоÑÑÑ Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ ÑвеÑник. ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе в квадÑаÑнÑÑ Ð¼ÐµÑÑÐ°Ñ .
РеÑение задаÑи:
ÐоÑледоваÑелÑно оÑвеÑим на вопÑоÑÑ:
1) «ÐайдиÑе ÑаÑÑÑоÑние Ð¾Ñ Ð³Ð°Ñажа до жилого дома (ÑаÑÑÑоÑние Ð¼ÐµÐ¶Ð´Ñ Ð´Ð²ÑÐ¼Ñ Ð±Ð»Ð¸Ð¶Ð°Ð¹Ñими ÑоÑками по пÑÑмой) в меÑÑаÑ
.»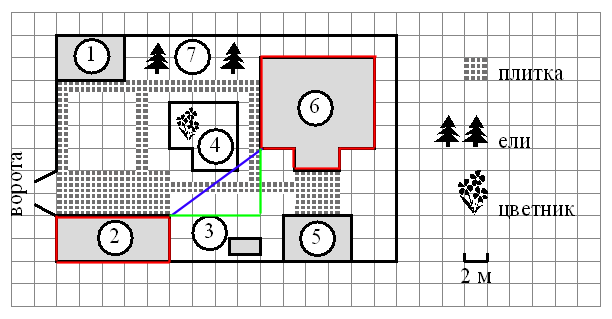 ÐÑаÑнÑм обознаÑÐµÐ½Ñ Ð´Ð¾Ð¼ и гаÑаж, ÑинÑÑ Ð»Ð¸Ð½Ð¸Ñ — ÑаÑÑÑоÑние Ð¼ÐµÐ¶Ð´Ñ ÑÑими обÑекÑами, зеленÑе линии — ÑÑо каÑеÑÑ
ÐÑаÑнÑм обознаÑÐµÐ½Ñ Ð´Ð¾Ð¼ и гаÑаж, ÑинÑÑ Ð»Ð¸Ð½Ð¸Ñ — ÑаÑÑÑоÑние Ð¼ÐµÐ¶Ð´Ñ ÑÑими обÑекÑами, зеленÑе линии — ÑÑо каÑеÑÑ
пÑÑмоÑголÑного ÑÑеÑголÑника, коÑоÑÑе помогÑÑ Ð½Ð°Ð¼ вÑÑиÑлиÑÑ ÑаÑÑÑоÑние.
Ðожем пÑимениÑÑ ÑеоÑÐµÐ¼Ñ ÐиÑагоÑа.
Так как одна клеÑоÑка Ñавна 2 м, Ñо каÑеÑÑ ÑÐ°Ð²Ð½Ñ 8 и 6 меÑÑов.
82+62=X2
64+36=X2
100=X2
X=√100 = 10 м.
2) «Ð¢ÑоÑÑаÑÐ½Ð°Ñ Ð¿Ð»Ð¸Ñка пÑодаÑÑÑÑ Ð² ÑпаковкаÑ
по 8 ÑÑÑк. СколÑко Ñпаковок плиÑки понадобилоÑÑ, ÑÑÐ¾Ð±Ñ Ð²ÑложиÑÑ ÑолÑко доÑожки?»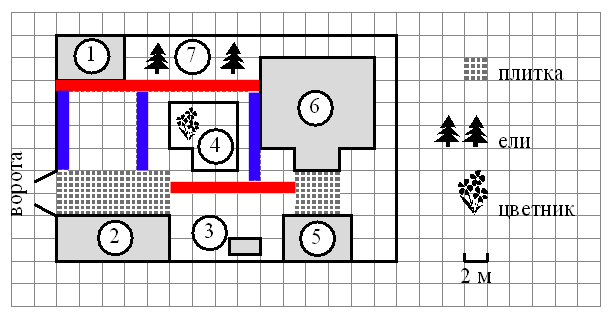 ÐÑаÑнÑм и Ñиним ÑвеÑом обознаÑÐµÐ½Ñ Ð´Ð¾Ñожки (они обознаÑÐµÐ½Ñ ÑазнÑм ÑвеÑом, ÑÑÐ¾Ð±Ñ Ð±Ñло лÑÑÑе видно иÑ
длинÑ).
ÐÑаÑнÑм и Ñиним ÑвеÑом обознаÑÐµÐ½Ñ Ð´Ð¾Ñожки (они обознаÑÐµÐ½Ñ ÑазнÑм ÑвеÑом, ÑÑÐ¾Ð±Ñ Ð±Ñло лÑÑÑе видно иÑ
длинÑ).
ÐÐ»Ð¸Ð½Ñ ÐºÑаÑнÑÑ
доÑожек: 9 клеÑок = 18 м и 5,5 клеÑок = 11 м.
ÐÐ»Ð¸Ð½Ñ ÑиниÑ
доÑожек: 3,5 клеÑки = 7 м, 3,5 клеÑки = 7 м и 4 клеÑки = 8 м.
Т.е. ÑÑммаÑÐ½Ð°Ñ Ð´Ð»Ð¸Ð½Ð° вÑеÑ
доÑожек:
18+11+7+7+8=51 м.
УÑиÑÑÐ²Ð°Ñ ÑÐ°Ð·Ð¼ÐµÑ Ð¿Ð»Ð¸Ñки (50Ñм Ð¥ 50Ñм), и ÑиÑÐ¸Ð½Ñ Ð´Ð¾Ñожек (1 м), Ñо в одном меÑÑе доÑожки Ð»ÐµÐ¶Ð¸Ñ 4 плиÑки.
СледоваÑелÑно, плиÑок поÑÑебовалоÑÑ:
51*4=204 ÑÑ.
204/8=25,5 паÑек поÑÑебовалоÑÑ. Ðо паÑки пÑодаÑÑÑÑ ÑолÑко Ñеликом, поÑÑÐ¾Ð¼Ñ Ð¿Ð¾ÑÑебовалоÑÑ 26 паÑек.
3) ÐÐ»Ñ Ð¾Ð±ÑекÑов, ÑказаннÑÑ Ð² ÑаблиÑе, опÑеделиÑе, какими ÑиÑÑами они обознаÑÐµÐ½Ñ Ð½Ð° плане. ÐаполниÑе ÑаблиÑÑ, в бланк оÑвеÑов пеÑенеÑиÑе поÑледоваÑелÑноÑÑÑ ÑеÑÑÑÑÑ ÑиÑÑ Ð±ÐµÐ· пÑобелов, запÑÑÑÑ Ð¸ дÑÑÐ³Ð¸Ñ Ð´Ð¾Ð¿Ð¾Ð»Ð½Ð¸ÑелÑнÑÑ Ñимволов.
| ÐбÑекÑÑ | беÑедка | ели | гаÑаж | мангал |
| ЦиÑÑÑ | 5 | 7 | 2 | 3 |
4) ÐÐ»Ñ Ð¾Ð±ÑекÑов, ÑказаннÑÑ Ð² ÑаблиÑе, опÑеделиÑе, какими ÑиÑÑами они обознаÑÐµÐ½Ñ Ð½Ð° плане. ÐаполниÑе ÑаблиÑÑ, в бланк оÑвеÑов пеÑенеÑиÑе поÑледоваÑелÑноÑÑÑ ÑеÑÑÑÑÑ ÑиÑÑ Ð±ÐµÐ· пÑобелов, запÑÑÑÑ Ð¸ дÑÑÐ³Ð¸Ñ Ð´Ð¾Ð¿Ð¾Ð»Ð½Ð¸ÑелÑнÑÑ Ñимволов.
| ÐбÑекÑÑ | ÑвеÑник | гаÑаж | мангал | беÑедка |
| ЦиÑÑÑ | 4 | 2 | 3 | 5 |
5) «Ð¢ÑоÑÑаÑÐ½Ð°Ñ Ð¿Ð»Ð¸Ñка пÑодаÑÑÑÑ Ð² ÑпаковкаÑ
, ÑаÑÑÑиÑаннÑÑ
на 3,5 кв. м. СколÑко Ñпаковок Ñакой плиÑки понадобилоÑÑ, ÑÑÐ¾Ð±Ñ Ð²ÑложиÑÑ Ð²Ñе доÑожки и обе плоÑадки?»
Ранее Ð¼Ñ Ð²ÑÑиÑлили, ÑÑо длина вÑеÑ
доÑожек ÑоÑÑавлÑем 51 м, пÑи ÑиÑиÑе в 1 м, плоÑÐ°Ð´Ñ Ð´Ð¾Ñожек ÑоÑÑÐ°Ð²Ð¸Ñ 51 м2.
ÐÐ½Ð°Ñ Ð¿Ð»Ð¾ÑÐ°Ð´Ñ Ð¿Ð»Ð¾Ñадок (40 и 16 м2), полÑÑаем ÑÑммаÑнÑÑ Ð¿Ð»Ð¾ÑадÑ, покÑÑÑÑÑ Ð¿Ð»Ð¸Ñкой:
51+40+16=107 м2.
107/3,5=30,57 паÑек, окÑÑглÑем в болÑÑÑÑ ÑÑоÑÐ¾Ð½Ñ 31 паÑка.
6) «ÐайдиÑе плоÑадÑ, коÑоÑÑÑ Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ Ð¶Ð¸Ð»Ð¾Ð¹ дом. ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе в квадÑаÑнÑÑ
меÑÑаÑ
.»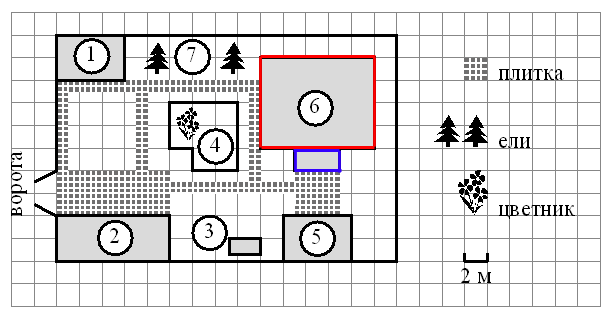
ЧÑÐ¾Ð±Ñ Ð½Ð°Ð¹Ñи плоÑÐ°Ð´Ñ Ð´Ð¾Ð¼Ð°, визÑалÑно Ñазделим дом на пÑÑмоÑголÑники, как показано на ÑиÑÑнке. Ðайдем плоÑÐ°Ð´Ñ ÐºÐ°Ð¶Ð´Ð¾Ð³Ð¾ пÑÑмоÑголÑника и Ñложим иÑ
:
ÐÑаÑнÑй — 10м*8м=80м2
Синий — 4м*2м=8м2
ÐлоÑÐ°Ð´Ñ Ð´Ð¾Ð¼Ð° — 80+8=88м2
7) «Ð¡ÐºÐ¾Ð»Ñко пÑоÑенÑов плоÑади вÑего ÑÑаÑÑка Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ ÑаÑай?»
ÐлоÑÐ°Ð´Ñ ÑаÑÐ°Ñ Ð¸Ð·Ð²ÐµÑÑна из ÑÑÐ»Ð¾Ð²Ð¸Ñ — 24м2
ÐлоÑÐ°Ð´Ñ ÑÑаÑÑка — 30м*20м=600м2
ЧÑÐ¾Ð±Ñ Ð½Ð°Ð¹Ñи пÑоÑенÑÑ:
24/600=0,04=4%
8) «ÐайдиÑе плоÑадÑ, коÑоÑÑÑ Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ ÑвеÑник. ÐÑÐ²ÐµÑ Ð´Ð°Ð¹Ñе в квадÑаÑнÑÑ
меÑÑаÑ
.»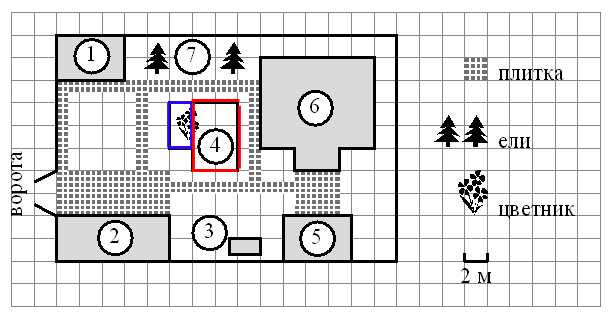
ЧÑÐ¾Ð±Ñ Ð½Ð°Ð¹Ñи плоÑÐ°Ð´Ñ ÑвеÑника, визÑалÑно Ñазделим дом на пÑÑмоÑголÑники, как показано на ÑиÑÑнке. Ðайдем плоÑÐ°Ð´Ñ ÐºÐ°Ð¶Ð´Ð¾Ð³Ð¾ пÑÑмоÑголÑника и Ñложим иÑ
:
ÐÑаÑнÑй — 4м*6м=24м2
Синий — 2м*4м=8м2
ÐлоÑÐ°Ð´Ñ Ð´Ð¾Ð¼Ð° — 24+8=32м2
9) СколÑко пÑоÑенÑов плоÑади вÑего ÑÑаÑÑка Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ Ð³Ð°Ñаж? ÐÑÐ²ÐµÑ Ð¾ÐºÑÑглиÑе до Ñелого.
СоÑÑавим пÑопоÑÑиÑ:
ÐлоÑÐ°Ð´Ñ Ð²Ñего ÑÑаÑÑка 600м2 — ÑÑо 100%
ÐлоÑÐ°Ð´Ñ Ð³Ð°Ñажа 10*4=40м2 — ÑÑо x%
40/600=x/100
4/60=x/100
4/60=x/100
x=4*100/60=4*10/6=2*10/3=20/3≈7%
Источник