Ступенчатый брус построить эпюры продольных сил и нормальных напряжений
Построение эпюр продольных сил — формулы, условия и примеры решения задач
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
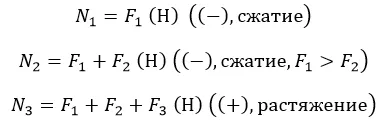
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
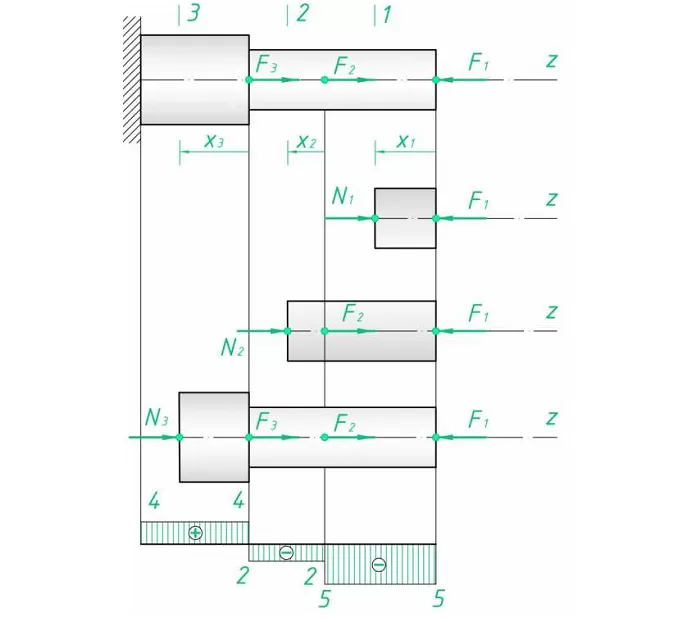
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
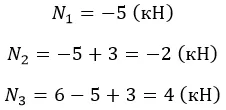
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
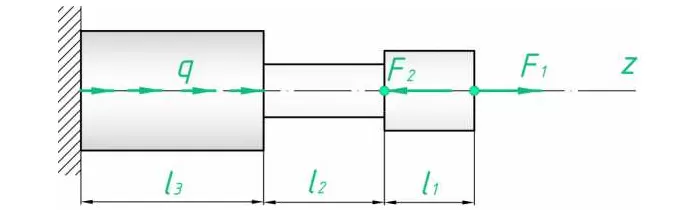
Рис. 2
Дано:
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
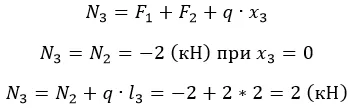
По полученным данным строим эпюру (рис. 3).
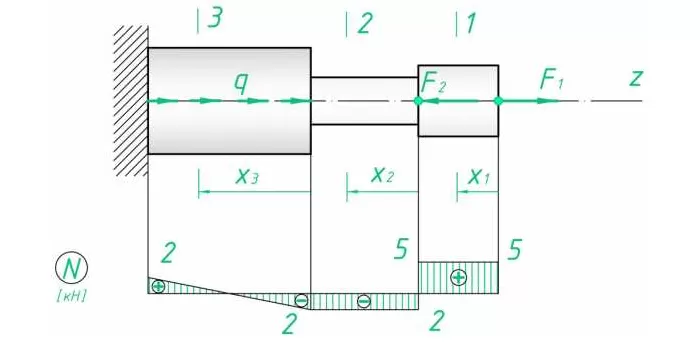
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
Тема: Построение эпюр продольных сил и нормальных напряжений
Время выполнения работы – 2 часа
Цель: Двухступенчатый стальной брус, длина ступеней которого указана на схеме, нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв МПа.
Задача:Числовые значения сил F1 и F2, а так же площадей поперечных сечений ступеней А1 и А2 взять из таблицы.
| Вариант | № схемы | F1,кН | F2,кН | А1, см2 | А2, см2 | Вариант | № схемы | F1,кН | F2,кН | А1, см2 | А2, см2 |
| IX | 22,0 | 30,6 | 2,7 | 2,1 | VI | 3,0 | 6,0 | 0,5 | 0,9 | ||
| VII | 16,0 | 8,0 | 1,4 | 0,4 | IV | 8,0 | 18,0 | 2,0 | 3,0 | ||
| V | 3,5 | 12,0 | 2,5 | 1,8 | II | 4,0 | 9,2 | 0,5 | 0,6 | ||
| III | 15,0 | 30,0 | 2,1 | 1,6 | IX | 12,0 | 34,0 | 2,2 | 1,8 | ||
| I | 10,0 | 20,0 | 1,2 | 0,8 | VII | 19,0 | 9,8 | 0,9 | 0,6 | ||
| X | 12,0 | 30,0 | 2,1 | 2,5 | V | 18,0 | 38,0 | 3,0 | 1,8 | ||
| VIII | 14,0 | 16,0 | 2,4 | 2,8 | III | 20,0 | 32,0 | 2,5 | 2,2 | ||
| VI | 6,0 | 3,0 | 0,4 | 0,8 | I | 12,0 | 20,0 | 0,7 | 0,9 | ||
| IV | 10,8 | 29,0 | 1,8 | 2,0 | X | 14,2 | 30,0 | 1,5 | 2,4 | ||
| II | 3,3 | 8,0 | 0,4 | 0,5 | VIII | 10,0 | 16,0 | 2,2 | 3,0 | ||
| IX | 10,8 | 30,0 | 2,8 | 2,4 | VI | 6,0 | 3,0 | 0,4 | 0,8 | ||
| VII | 8,3 | 30,5 | 1,5 | 0,8 | IV | 7,6 | 20,5 | 2,8 | 3,2 | ||
| V | 27,0 | 27,0 | 2,8 | 2,0 | II | 4,8 | 10,0 | 0,4 | 0,8 | ||
| III | 14,0 | 18,0 | 2,3 | 2,1 | IX | 11,0 | 24,0 | 2,0 | 1,6 | ||
| I | 12,0 | 10,0 | 1,2 | 0,8 | VII | 8,0 | 8,4 | 2,0 | 1,4 | ||
| X | 14,0 | 40,0 | 2,0 | 2,0 | V | 1,4 | 20,0 | 2,6 | 1,5 | ||
| VIII | 16,0 | 12,0 | 1,1 | 3,0 | III | 30,0 | 36,0 | 2,4 | 1,6 |
Практическая работа №8
Тема: Решение задач по теме «Растяжение , сжатие»
Время выполнения работы – 1 час
Растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении стержня возникает один внутренний силовой фактор – продольная сила N.
Величина последней равна алгебраической сумме проекций на продольную ось внешних сил, действующих на отсеченную часть стержня
N=∑ FKZ (1)
Так как величина продольных сил в разных сечениях стержня неодинакова, то строится эпюра продольных сил, т.е. график, показывающий изменения величины продольных сил в сечении стержня по его длине.
Под действием продольных сил в поперечном сечении стержня возникает нормальное напряжение, которое определяется по формуле:
σ =N/А
где А- площадь поперечного сечения стержня.
При решении первой задачи от студента требуется умение строить эпюры продольных сил, нормальных напряжений и определять удлинение или укорочение стержня.
Последовательность построения эпюр продольных сил:
Разбиваем стержень на участки, ограниченные точками приложения сил ( нумерацию участков ведём от незакрепленного конца ).
Используя метод сечений, определяем величину продольных сил в сечении каждого участка.
Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением стержня проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответственно в выбранном масштабе продольным силам (положительное значение откладываем вверх ( или в право ) отрицательное — вниз ( или влево).
Последовательность построения эпюр нормальных напряжений.
Разбиваем стержень на участки, ограниченные точками приложения сил и там, где меняется площадь сечения
Строим эпюру нормальных сил
по формуле 1 определяем нормальные напряжения на каждом участке
По полученным значениям в масштабе строим эпюру нормальных напряжений.
Удлинение ( укорочение ) стержня определяется по формуле Гука .
где Е – модуль Юнга ( для стали Е=2·10 5 МПа ).
Удлинение (укорочение) определяется на каждом участке стержня, а затем находят алгебраическую сумму полученных значений. Это будет ∆lстержня. Если ∆l положительна, то брус удлиняется, если ∆l отрицательна, то укорачивается.
При решении ряда задач необходимо ясно представлять смысл условия прочности при растяжении – сжатии, знать, что исходя из условия прочности, можно производить три вида расчётов:
а) проверочный, при котором проверяется выполнено ли условие прочности σ≤ [σ] ( или n≥ [n]);
б) определение допускаемой нагрузки;
в) проектный, при котором определяются необходимые размеры поперечных сечений бруса, обеспечивающие заданную прочность.
Студенты должны также уметь пользоваться в ходе решения всеми необходимыми формулами, расчётными зависимостями и правильно выполнять вычисления.
II. Вопросы для самопроверки
2.1. Как нужно нагрузить прямой брус, чтобы он работал на растяжение — сжатие?
2.2 Как определяется напряжение в любой точке поперечного сечения при растяжении (сжатии)?
2.3. Каков физический смысл модуля продольной упругости Е?
2.4. Что такое допускаемое напряжение и как оно выбирается в зависимости от механических свойств материала?
2.5. Сколько различных видов расчёта, и какие расчеты можно проводить, используя условие прочности?
адача. Проверить прочность стального стержня при заданых допускаемых напряжениях 160МПа. (решение задач по технической механике)
А лгоритм решения
- Находим неизвестные внешние усилия (силы, моменты, реакции опор)
- Разбиваем на расчетные участки (границы расчетных участков определяются изменением нагрузки, площади сечения, материала).
- Пользуясь методом сечений определяем продольные силы. (Метод сечений: Разрезаем стержень, Отбрасываем одну из частей, Заменяем действие отброшенной части внутренними силами, составляем Уравнения равновесия рассматриваемой части)
- Строим эпюру продольных сил
- определяем нормальные напряжения на участках
- Строим эпюру перемещений
- Проверяем прочность стержня (в случае, если материал стержня по разному работает на растяжениеи сжатие, проверяем прочность отдельно на растяжения и сжатие)
- Определяем перемещения на каждом участке (перемещение в конце участка равняется сумме перемещений в начале участка и перемещению на данном участке)
9. Строим эпюру перемещений
При решении задачи пренебрегаем собственным весом стержя.
При жестко закрепленном стержне вначале можно не определять реакции в опоре, а строить эпюры, идя со свободного конца стержня. При этом реакцию в опоре можно определить по эпюре продольных сил
Порядок решения типовых задач
Задача №1
Двухступенчатый стальной брус нагружен силами F1=30 кН F2=40 кН.
Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆l свободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=1,5см2?;А 2 =2см2?
Первая задача требует от студента умения строить эпюры продольных сил, нормальных напряжений и определять удлинения и укорочения бруса.
Последовательность решения задачи
Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.
Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.
Перемещение свободного конча бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
Решение:
Разбиваем брус на участки.
Определяем ординаты эпюры N на участках бруса:
N1= — F1= -30кН
N2= — F2= -30кН
N3= -F1+F2= -30+40=10 кН
Строим эпюру продольных сил
Вычисляем ординаты эпюры нормальных напряжений
σ1 = = = –200МПа
σ2 = = = –150МПа
σ 3=== 50МПа
Строим эпюры нормальных напряжений.
4. Определяем перемещение свободного конца бруса
∆l=∆l1+∆l2+∆l3
∆l1= = = – 0,5мм
∆l2= = = – 0,225мм
∆l3= = = 0,05мм
∆l= — 0,5 – 0,225 + 0,05 = – 0,675мм
Брус укоротился на 0,675мм
Задача № 2
Из условия прочности определить размеры поперечного сечения стержня, удерживающего в равновесии балку, если предел текучести материала σ т=320МПа, заданный коэффициент запаса прочности [n] = 2,5. Расчет провести для двух случаев:
1. поперечное сечение стержня – круг;
2. поперечное сечение стержня – квадрат.
Вторая задача может быть решена студентами, если они будут ясно представлять смысл условия прочности при растяжении (сжатии).
Последовательность решения задачи:
Балку, равновесие которой рассматривается, освободить от связей и заменить действия связей их реакциями;
Составить уравнение равновесия, причем принять за точку, относительно которой определяются моменты, точку в которой установлена опора, и определяем продольную силу N;
Определить из условия прочности площадь поперечного сечения стержня;
Определить для двух случаев размеры поперечного сечения стержня.
Для круга – диаметр d;
Для квадрата – сторону a.
Решение
Составляем уравнение равновесия и определяем продольную силу N
Σ m A=0
N∙sin30°∙3 – 3q∙1,5 + F∙1 = 0
N= = = 53,3 кН
2. Определяем допускаемое нормальное напряжение
[σ]= | σ | = = 128 МПа |
| [n] |
3. Определяем площадь поперечного сечения стержня
σmax | = | N | ≤ [σ]→A ≥ | N | = | 53,3∙103 | =416 мм2 |
| A | [σ] | 128 |
4. Определяем размеры попе речного сечения круга – диаметр d
А= →d= = = 23 мм
5. Определяем размеры поперечного сечения квадрата – сторону a
A=a2→a= = = 20,4 мм.
IV. Задания для самостоятельного решения
Задача №1
Проверить прочность стальной тяги ВО диаметром d=20мм,если предел текучести σт =240МПа.требуемый коэффициент запаса прочности [n]=1,5
Ответ: перегружена на 58,75%
Задача 2.
Проверить прочность стальных брусьев, если [σ]=160МПа
Ответ: а) перегружен на 4,4%
б) недогружен на 7,5%
Задача 3.
Определить требуемую площадь А поперечного сечения стального бруса, если [σ]=160МПа,
Ответ: а) А=188мм2
б) А=90,6мм2
Задача№4
Определить допускаемую нагрузку для стального стержня, если σт =250МПа, [n]=1,6
Ответ: [F]=31,2кН
Задача №5
Определить размеры поперечного сечения стержня кронштейна, если [σр]=160МПа, [σсж]=120МПа
Ответ: а=10мм,d=10мм.
Практическая работа №9
Источник
Ознакомиться с примером построения эпюр продольных сил, напряжений и перемещений.
Тема: Решение задач на построение эпюр нормальных сил, нормальных напряжений, перемещений сечений бруса.
Ознакомиться с примером построения эпюр продольных сил, напряжений и перемещений.
Задача 1.Двухступенчатый стальной брус нагружен силами F1=30 кН F2=40 кН.
Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=1,5см2;А 2=2см2.
Решение.
Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.
Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.
Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.
Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.
Разбиваем брус на участки.
Определяем ординаты эпюры N на участках бруса:
N1= — F1= -30кН
N2= — F2= -30кН
N3= -F1+F2= -30+40=10 кН
Строим эпюру продольных сил
Вычисляем ординаты эпюры нормальных напряжений
σ1 = = = –200МПа
σ2 = = = –150МПа
σ 3= = =50МПа
Строим эпюры нормальных напряжений.
4. Проверяем прочность бруса, если допускаемое напряжение [σ] = 160 МПа.
Выбираем максимальное по модулю расчетное напряжение. IσmaxI = 200 МПа
Подставляем в условие прочности IσmaxI ≤ [σ]
200 МПа ≤ 160 МПа. Делаем вывод, что прочность не обеспечена.
5. Определяем перемещение свободного конца бруса Е = 2∙10 5 МПа.
∆l=∆l1+∆l2+∆l3
∆l1= = = – 0,5мм
∆l2= = = – 0,225мм
∆l3= = = 0,05мм
∆l= — 0,5 – 0,225 + 0,05 = – 0,675мм
Брус укоротился на 0,675мм
1. Задание: Решить задачи
Двухступенчатый стальной брус нагружен силами F1, F2.
Построить эпюры продольных сил и нормальных напряжений по длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆lсвободного конца бруса, приняв Е=2∙10 5 МПа. Площади поперечных сечений А1=5 см2;А 2 =10 см2. Длина l = 0,5 м. Первая команда F1= 50 кН, F2 = 30 кН. Вторая команда F1= 30 кН, F2 = 50 кН.
F1
l l l
l l l
Разбить брус на участки. Пронумеровать эти участки.
Найти величину продольной силы на первом участке.
Найти величину продольной силы на втором участке.
Найти величину продольной силы на третьем участке.
Построить эпюру для продольной силы.
Найти величину нормального напряжения на первом участке.
Найти величину нормального напряжения на втором участке.
Найти величину нормального напряжения на третьем участке.
Построить эпюру для нормального напряжения.
Проверить прочность бруса. Допускаемое напряжение [σ] = 160 МПа.
Определить перемещение свободного конца бруса.
Задание 2
Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.
Задание 3
Для стального прямого бруса построить эпюры продольных сил и нормальных напряжений. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа.
Литература
В.П. Олофинская «Техническая механика» курс лекций с вариантами практических и тестовых заданий.
Лекции по теме (конспекты).

Источник
Примеры построения эпюры продольных сил
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а).
Делим брус на участки нагружения.
Участком нагружения считают часть бруса между внешними силами.
Тема 2.2. Растяжение и сжатие 177
На представленном рисунке 3 участка нагружения. Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Участок 1: ∑ Fz = 0; —3F + N 1 = 0; N 1 = 3F. Продольная сила положительна, участок 1 растянут.
Участок 2: ∑ Fz = 0; -3F + 2F + N 2 = 0; N 2 = F . Продольная сила положительна, участок 2 растянут.
Участок 3: ∑ Fz= 0; -3F + 2F + 5F — N3 = 0; N 3 = 4F . Продольная сила отрицательна, участок 3 сжат. Полученное значение N 3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.26).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz .
Правило контроля: в месте приложения внешней силы на эпюре должен быть скачок на величину приложенной силы.
178 Лекция 20
На эпюре проставляются значения Nz . Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
Изучая деформации при растяжении и сжатии, обнаруживаем, что выполняются гипотеза плоских сечений и принцип смягчения граничных условий.
Гипотеза плоских сечений заключается в том, что поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
Следовательно, продольные внутренние волокна удлиняются одинаково, а внутренние силы упругости распределены по сечению равномерно.
Принцип смягчения граничных условий гласит: в точках тела, удаленных от мест приложения нагрузки, модуль внутренних сил мало зависит от способа закрепления. Поэтому при решении задач не уточняют способ закрепления.
Напряжения при растяжении и сжатии
При растяжении и сжатии в сечении действует только нормальное напряжение.
Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади.
Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис. 20.3).
Исходя из гипотезы плоских сечений, можно предположить, что напряжения при растяжении и сжатии в пределах каждого сечения не меняются. Поэтому напряжение можно рассчитать по формуле
где Nz— продольная cила в сечении; А — площадь поперечного сечения.
Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.
Нормальные напряжения действуют при растяжении от сечения (рис. 20.4а), а при сжатии к сечению (рис. 20.46).
Тема 2.2. Растяжение и сжатие 179
Размерность (единица измерения) напряжений — Н/м2 (Па), однако это слишком малая единица, и практически напряжения рассчитывают в Н/мм2 (МПа):При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений.
Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
Рассмотрим брус, нагруженный внешними силами вдоль оси (рис. 20.5).
Обнаруживаем три участка нагружения и определяем величины продольных сил.
Участок 1: N 1 = 0. Внутренние продольные силы равны нулю.
Участок 2: N 2= 2F . Продольная сила на участке положительна.
Участок 3: N3= 2F-3F = — F . Продольная сила на участке отрицательна.
Брус — ступенчатый. С учетом изменений величин площади поперечного сечения участков напряжений больше.
Строим эпюры продольных сил и нормальных напряжений. Масштабы эпюр могут быть разными и выбираются исходя из удобства построения.
180 Лекция 20
Примеры решения задач
Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.
Решение
1. Определяем участки нагружения, их два.
2. Определяем продольную силу в сечениях 1 и 2.
3. Строим эпюру.
4. Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.
1. Определяем продольные силы.
Тема 2.2. Растяжение и сжатие 181
Сечение 1. – N1 + F1= 0; N1 = F1= 100 кН.
Сечение 2. -80 — N 2 + 100 = 0; N 2= 100 — 80 = 20 кН.
В обоих сечениях продольные силы положительны.
Nz
2. Определяем нормальные напряжения σ = — .
A
Сопоставляя участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений. Нормальные напряжения в сечениях по участкам:
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Контрольные вопросы и задания
1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
2. Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений.)
3. Какого характера напряжения возникают в поперечном сечении при растяжении и сжатии: нормальные или касательные?
4. Как распределены напряжения по сечению при растяжении и
сжатии?
5. Запишите формулу для расчета нормальных напряжений при
растяжении и сжатии.
6. Как назначаются знаки продольной силы и нормального напряжения?
7. Что показывает эпюра продольной силы?
8. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
9. В каких единицах измеряется напряжение?
182 Лекция 21
ЛЕКЦИЯ 21
Источник